
【题目】将函数![]() 的图象的纵坐标不变,横坐标缩短为原来的
的图象的纵坐标不变,横坐标缩短为原来的![]() ,得到函数
,得到函数![]() 的图象.已知函数
的图象.已知函数![]() .
.
(1)若函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,求
,求![]() 的值;
的值;
(2)设函数![]() ,证明:对任意
,证明:对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 在
在![]() 上恒成立.
上恒成立.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() ,某抛物线的顶点为原点
,某抛物线的顶点为原点![]() ,焦点为圆心
,焦点为圆心![]() ,经过点
,经过点![]() 的直线
的直线![]() 交圆
交圆![]() 于
于![]() ,
, ![]() 两点,交此抛物线于
两点,交此抛物线于![]() ,
, ![]() 两点,其中
两点,其中![]() ,
, ![]() 在第一象限,
在第一象限, ![]() ,
, ![]() 在第二象限.
在第二象限.
(1)求该抛物线的方程;
(2)是否存在直线![]() ,使
,使![]() 是
是![]() 与
与![]() 的等差中项?若存在,求直线
的等差中项?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
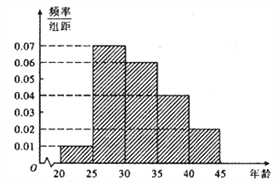
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
(1)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
 (2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
(2)在(1)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某企业有甲、乙两个研发小组.为了比较他们的研发水平,现随机抽取这两个小组往年研发新产品的结果如下:(a,b),(a,![]() ),(a,b),(
),(a,b),(![]() ,b),(
,b),(![]() ,
,![]() ),(a,b),(a,b),(a,
),(a,b),(a,b),(a,![]() ),(
),(![]() ,b),(a,
,b),(a,![]() ),(
),(![]() ,
,![]() ),(a,b),(a,
),(a,b),(a,![]() ),(
),(![]() ,b),(a,b).其中a,
,b),(a,b).其中a,![]() 分别表示甲组研发成功和失败;b,
分别表示甲组研发成功和失败;b,![]() 分别表示乙组研发成功和失败.
分别表示乙组研发成功和失败.
(I)若某组成功研发一种新产品,则给该组记1分,否则记0分.试计算甲、乙两组研发新产品的成绩的平均数和方差,并比较甲、乙两组的研发水平;
(II)若该企业安排甲、乙两组各自研发一种新产品,试估计恰有一组研发成功的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在[﹣1,1]上的函数f(x)满足:①对任意a,b∈[﹣1,1],且a+b≠0,都有 ![]() >0成立;②f(x)在[﹣1,1]上是奇函数,且f(1)=1.
>0成立;②f(x)在[﹣1,1]上是奇函数,且f(1)=1.
(1)求证:f(x)在[﹣1,1]上是单调递增函数;
(2)解关于x不等式f(x)<f( ![]() x+1);
x+1);
(3)若f(x)≤m2﹣2am﹣2对所有的x∈[﹣1,1]及a∈[﹣1,1]恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校5个学生的数学和物理成绩如表
学生的编号i | 1 | 2 | 3 | 4 | 5 |
数学xi | 80 | 75 | 70 | 65 | 60 |
物理yi | 70 | 66 | 68 | 64 | 62 |
(Ⅰ)假设在对这5名学生成绩进行统计时,把这5名学生的物理成绩搞乱了,数学成绩没出现问题,问:恰有2名学生的物理成绩是自己的实际分数的概率是多少?
(Ⅱ)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系的,在上述表格是正确的前提下,用x表示数学成绩,用y表示物理成绩,求y与x的回归方程;
参考公式: ![]() =
= 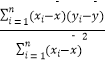 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,已知向量 ![]() =(﹣1,2),又点A(8,0),B(n,t),C(ksinθ,t),θ∈R.
=(﹣1,2),又点A(8,0),B(n,t),C(ksinθ,t),θ∈R.
(1)若 ![]() ⊥
⊥ ![]() ,且
,且 ![]() ,求向量
,求向量 ![]() ;
;
(2)若向量 ![]() 与向量
与向量 ![]() 共线,常数k>0,求f(θ)=tsinθ的值域.
共线,常数k>0,求f(θ)=tsinθ的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(Ⅰ)设z=1+i(i是虚数单位),求 ![]() +z2的值; (Ⅱ)设x,y∈R,复数z=x+yi,且满足|z|2+(z+
+z2的值; (Ⅱ)设x,y∈R,复数z=x+yi,且满足|z|2+(z+ ![]() )i=
)i= ![]() ,试求x,y的值.
,试求x,y的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com