
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | $\frac{9\sqrt{3}}{4}$ | D. | $\frac{27\sqrt{3}}{4}$ |
分析 可作正三棱锥S-ABC,取底面中心为O,BC中点为D,连接SO,BO,OD,容易说明∠SBO=60°,并且∠OBD=30°,从而根据侧棱长可以分别求出该正三棱锥的高SO,底面正三角形的边长,从而可以求出底面面积,根据三棱锥的体积公式即可得出该三棱锥的体积.
解答 解:如图,正三棱锥S-ABC,底面中心为O,取BC中点D,连接SO,BO,OD,则:
SO⊥底面ABC,OD⊥BC;
∴∠SBO为侧棱SB和底面ABC所成角为60°;
∴∠SBO=60°,SB=$2\sqrt{3}$;
∴在RT△SBO中,OB=$SB•cos60°=\sqrt{3}$,SO=SB•sin60°=3;
∴$BD=OB•cos30°=\frac{3}{2}$,BC=3;
∴${S}_{△ABC}=\frac{1}{2}•3•3•sin60°=\frac{9\sqrt{3}}{4}$;
∴${V}_{三棱锥S-ABC}=\frac{1}{3}{S}_{△ABC}•SO$=$\frac{1}{3}×\frac{9\sqrt{3}}{4}×3=\frac{9\sqrt{3}}{4}$.
故选:C.
点评 考查正三棱锥的定义,正三角形中心的概念,以及直线和平面所成角的概念并能找到直线和平面所成角,直角三角形边角的关系,以及三角形面积公式,三棱锥的体积公式.


科目:高中数学 来源: 题型:解答题
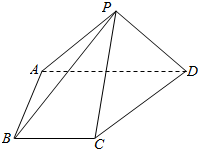 如图,四棱锥P-ABCD中,平面PAD⊥底面ABCD,PA⊥PD,PA=PD,BC∥AD,AB⊥AD,AD=2AB=2BC=2.
如图,四棱锥P-ABCD中,平面PAD⊥底面ABCD,PA⊥PD,PA=PD,BC∥AD,AB⊥AD,AD=2AB=2BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3) | B. | (1,2] | C. | [2,3) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$] | C. | (-∞,0)∪(0,$\frac{1}{2}$] | D. | [$\frac{1}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 高校 | 相关人数 | 抽取人数 |
| A | 15 | 1 |
| B | 30 | x |
| C | 60 | y |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com