
����Ŀ����֪����![]() .
.
��1���жϲ�֤������![]() ����ż�ԣ�
����ż�ԣ�
��2���жϵ�![]() ʱ����
ʱ����![]() �ĵ����ԣ����ö���֤����
�ĵ����ԣ����ö���֤����
��3����![]() ������Ϊ
������Ϊ![]() ���ⲻ��ʽ
���ⲻ��ʽ![]() .
.
���𰸡���1���溯����2����������3��![]()
�������������������1���ж���֤����������ż�ԣ�����Ҫȷ�������Ķ������Ƿ����ԭ��Գƣ����ж�f(-x)��f(x)�Ĺ�ϵ������Զ������ϵ�����x��������f(-x)=f(x)����ż���������f(-x)=-f(x)�����溯���������Ƿ����ż��������2�������������Զ���֤�������ԣ������裬��������жϣ��½���������衣��3���ɣ�1����2���溯��![]() �ڣ�-1��1��Ϊ����������
�ڣ�-1��1��Ϊ����������
ԭ����ʽ����Ϊf(2x-1)<-f(x),��f(2x-1)<f(-x),���ɺ����ĵ����Լ����壨-1��1������x��Χ��
�����������1������![]() Ϊ�溯����֤�����£�
Ϊ�溯����֤�����£�
![]() ������Ϊ
������Ϊ![]()
��![]()
![]() Ϊ�溯��
Ϊ�溯��
��2������![]() �ڣ�-1��1��Ϊ����������֤�����£�
�ڣ�-1��1��Ϊ����������֤�����£�
��ȡ![]() ����
����
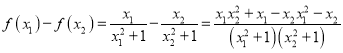
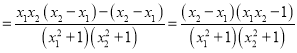
![]()
![]() ��
�� ![]()
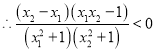
��![]()
��![]() �ڣ�-1��1����Ϊ������
�ڣ�-1��1����Ϊ������
��3���ɣ�1������2���ɵ�
![]() ��
��
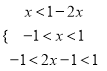 ��ã�
��ã� ![]()
���ԣ�ԭ����ʽ�Ľ⼯Ϊ![]()
���㾦��
��1����ż�ԣ��ж���֤����������ż�ԣ�����Ҫȷ�������Ķ������Ƿ����ԭ��Գƣ����ж�f(-x)��f(x)�Ĺ�ϵ������Զ������ϵ�����x��������f(-x)=f(x)����ż���������f(-x)=-f(x)�����溯���������Ƿ����ż������
��2�������ԣ������������Զ���֤�������ԣ������裬��������ţ��½���������衣
�����͡������
��������
22
����Ŀ����֪����![]() .
.
��1����![]() �Ķ������ֵ�����
�Ķ������ֵ�����![]() ����ʵ��
����ʵ��![]() ��ֵ��
��ֵ��
��2����![]() ������
������![]() ���Ǽ��������Ҷ������
���Ǽ��������Ҷ������![]() ������
������![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ���Ҷ������
���Ҷ������![]() ��������
��������![]() ��ʹ��
��ʹ��![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
���𰸡���1��![]() ��2��
��2��![]() ��3��
��3��![]()
�������������������1�������ö��κ���������ȷ������![]() �ĵ����ݼ�����Ϊ
�ĵ����ݼ�����Ϊ![]() ����
����![]() ��
��![]() �����ݼ���Ȼ���ɶ�������ֵ���г���ʽ��ϵ���Ӷ���⼴�ɣ���2���ɣ�1����֪
�����ݼ���Ȼ���ɶ�������ֵ���г���ʽ��ϵ���Ӷ���⼴�ɣ���2���ɣ�1����֪![]() ������ȷ��
������ȷ��![]() ��ȡֵ��Χ
��ȡֵ��Χ![]() ��Ȼ��ȷ��
��Ȼ��ȷ��![]() ʱ����
ʱ����![]() �����ֵ
�����ֵ![]() ��������ⲻ��ʽ��
��������ⲻ��ʽ��![]() ���ɣ���3�������������
���ɣ���3�������������![]() ��������
��������![]() ��ʹ��
��ʹ��![]() ������ת��Ϊ
������ת��Ϊ![]() ʱ��
ʱ��![]() ��ֵ�������
��ֵ�������![]() ��
��![]() ��ֵ��Ȼ����зֱ���
��ֵ��Ȼ����зֱ���![]() ��
��![]() ��ֵ�Ӽ��ϼ�İ�����ϵ�������
��ֵ�Ӽ��ϼ�İ�����ϵ�������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�����������1����![]()
��![]() ��
��![]() �ϵ����ݼ�����
�ϵ����ݼ�����![]() ����
����![]() ��
��![]() �ϵ����ݼ���
�ϵ����ݼ���
��![]() ����
����![]() ����
����![]() 4��
4��
��2����![]() ������
������![]() ���Ǽ���������
���Ǽ���������![]() ����
����![]()
��![]() ��
��![]()
��![]() ʱ��
ʱ��![]()
�����������![]() ������
������![]() ��
��
��![]() ����
����![]() ��Ҳ����
��Ҳ����![]()
���Ͽ�֪![]() 8��
8��
��3����![]() ��
��![]() �ϵ�����
�ϵ�����![]() ��
��![]() �ϵݼ���
�ϵݼ���
��![]() ʱ��
ʱ��![]() ��
��![]()
���������![]() ��������
��������![]() ��ʹ��
��ʹ��![]() ����
����
��![]()
![]()
��![]() ������
������![]() 13��
13��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���֪��P��0��1����ԲC��x2+y2+2mx��2y+m2��4m+1=0�ڣ������ڹ���P��ֱ�߽�ԲC��A��B���㣬�ҡ�PBC������ǡ�PAC�������2������ʵ��m��ȡֵ��ΧΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x2eax ��
����a��0ʱ�����ۺ���f��x���ĵ����ԣ�
�����ڣ�1�������£�����f��x��������[0��1]�ϵ����ֵ��
�����躯��g��x��=2ex�� ![]() ����֤����a=1����x�ʣ�0��1����g��x����xf��x����2�������
����֤����a=1����x�ʣ�0��1����g��x����xf��x����2�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]() .
.
��1������![]() �Ķ�����
�Ķ�����
��2���жϺ���![]() ����ż�ԣ���˵�����ɣ�
����ż�ԣ���˵�����ɣ�
��3���жϺ���![]() ������
������![]() �ϵĵ����ԣ�������֤��.
�ϵĵ����ԣ�������֤��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1���жϲ�֤������![]() ����ż�ԣ�
����ż�ԣ�
��2���жϵ�![]() ʱ����
ʱ����![]() �ĵ����ԣ����ö���֤����
�ĵ����ԣ����ö���֤����
��3����![]() ������Ϊ
������Ϊ![]() ���ⲻ��ʽ
���ⲻ��ʽ![]() .
.
���𰸡���1���溯����2����������3��![]()
�������������������1���ж���֤����������ż�ԣ�����Ҫȷ�������Ķ������Ƿ����ԭ��Գƣ����ж�f(-x)��f(x)�Ĺ�ϵ������Զ������ϵ�����x��������f(-x)=f(x)����ż���������f(-x)=-f(x)�����溯���������Ƿ����ż��������2�������������Զ���֤�������ԣ������裬��������жϣ��½���������衣��3���ɣ�1����2���溯��![]() �ڣ�-1��1��Ϊ����������
�ڣ�-1��1��Ϊ����������
ԭ����ʽ����Ϊf(2x-1)<-f(x),��f(2x-1)<f(-x),���ɺ����ĵ����Լ����壨-1��1������x��Χ��
�����������1������![]() Ϊ�溯����֤�����£�
Ϊ�溯����֤�����£�
![]() ������Ϊ
������Ϊ![]()
��![]()
![]() Ϊ�溯��
Ϊ�溯��
��2������![]() �ڣ�-1��1��Ϊ����������֤�����£�
�ڣ�-1��1��Ϊ����������֤�����£�
��ȡ![]() ����
����


![]()
![]() ��
�� ![]()

��![]()
��![]() �ڣ�-1��1����Ϊ������
�ڣ�-1��1����Ϊ������
��3���ɣ�1������2���ɵ�
![]() ��
��
 ��ã�
��ã� ![]()
���ԣ�ԭ����ʽ�Ľ⼯Ϊ![]()
���㾦��
��1����ż�ԣ��ж���֤����������ż�ԣ�����Ҫȷ�������Ķ������Ƿ����ԭ��Գƣ����ж�f(-x)��f(x)�Ĺ�ϵ������Զ������ϵ�����x��������f(-x)=f(x)����ż���������f(-x)=-f(x)�����溯���������Ƿ����ż������
��2�������ԣ������������Զ���֤�������ԣ������裬��������ţ��½���������衣
�����͡������
��������
22
����Ŀ����֪����![]() .
.
��1����![]() �Ķ������ֵ�����
�Ķ������ֵ�����![]() ����ʵ��
����ʵ��![]() ��ֵ��
��ֵ��
��2����![]() ������
������![]() ���Ǽ��������Ҷ������
���Ǽ��������Ҷ������![]() ������
������![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ���Ҷ������
���Ҷ������![]() ��������
��������![]() ��ʹ��
��ʹ��![]() ��������ʵ��
��������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������f��x��=Asin��x+�գ���A��0��0����4��|��|�� ![]() �����㣨0��
�����㣨0�� ![]() �����ҵ�x=
�����ҵ�x= ![]() ʱ������f��x��ȡ�����ֵ1��
ʱ������f��x��ȡ�����ֵ1��
��1��������f��x����ͼ������ƽ�� ![]() ����λ�õ�����g��x��������g��x���ı���ʽ��
����λ�õ�����g��x��������g��x���ı���ʽ��
��2���ڣ�1���������£�����h��x��=f��x��+g��x��+2cos2x��1���������x1 �� x2��R������h��x1����h��x����h��x2������|x1��x2|����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a1 �� a2 �� ����an��R��n��3����p��a1 �� a2 �� ����an�ɵȱ����У�q����a ![]() +a
+a ![]() +��+a
+��+a ![]() ����a
����a ![]() +a
+a ![]() +��+a
+��+a ![]() ��=��a1a2+a2a3+��+an1an��2 �� ��p��q��������
��=��a1a2+a2a3+��+an1an��2 �� ��p��q��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������CD��AB��ֱ������AB�ཻ�ڵ�E����FΪ��CD�����ڵ�E������һ�㣬����BF��AF���ӳ�����O�ڵ�M��N�� 
��1����֤��B��E��F��N�ĵ㹲Բ��
��2����֤��AC2+BFBM=AB2 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������R�ϵ��溯��f��x������x��0ʱ��
f��x��= ��
��
�����x�ĺ���F��x��=f��x����a��0��a��1�����������֮��Ϊ��������
A.1��2a
B.2a��1
C.1��2��a
D.2��a��1
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com