
分析 利用分数指数幂的运算法则和多项式乘以多项式的运算法则进行求解.
解答 解:4a${\;}^{\frac{2}{3}}$b${\;}^{-\frac{1}{3}}$÷(-$\frac{2}{3}$a${\;}^{-\frac{1}{3}}$b${\;}^{-\frac{1}{3}}$)
=4×(-$\frac{3}{2}$)${a}^{\frac{2}{3}-(-\frac{1}{3})}$${b}^{-\frac{1}{3}-(-\frac{1}{3})}$
=-6a.
(-2x${\;}^{\frac{1}{4}}$y${\;}^{-\frac{1}{3}}$)(3x${\;}^{-\frac{1}{2}}$y${\;}^{\frac{2}{3}}$)(-4x${\;}^{\frac{1}{4}}$y${\;}^{\frac{2}{3}}$)
=(-2)×3×(-4)${x}^{\frac{1}{4}-\frac{1}{2}+\frac{1}{4}}$${y}^{-\frac{1}{3}+\frac{2}{3}+\frac{2}{3}}$
=24y.
4x${\;}^{\frac{1}{4}}$(-3x${\;}^{\frac{1}{4}}$y${\;}^{-\frac{1}{3}}$)÷(-6x${\;}^{-\frac{1}{2}}$y${\;}^{-\frac{2}{3}}$)
=[4×(-3)÷(-6)]${x}^{\frac{1}{4}+\frac{1}{4}-(-\frac{1}{2})}$${y}^{-\frac{1}{3}-(-\frac{2}{3}})$
=2x${y}^{\frac{1}{3}}$.
点评 本题考查分数指数幂的化简求值,是基础题,解题时要认真审题,注意分数指数幂的运算法则和多项式乘以多项式的运算法则的合理运用.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
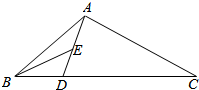 如图,在△ABC中,AB=AC=1,cos∠BAC=$\frac{1}{3}$,D是BC上一点,且DC=2BD,E是AD的中点,则BE的长为$\frac{\sqrt{129}}{18}$.
如图,在△ABC中,AB=AC=1,cos∠BAC=$\frac{1}{3}$,D是BC上一点,且DC=2BD,E是AD的中点,则BE的长为$\frac{\sqrt{129}}{18}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com