
分析 由已知利用基本不等式求出x+2y的最小值,代入m2-2m≤8求得m的范围得答案.
解答 解:∵x>0,y>0,且$\frac{2}{x}+\frac{1}{y}=1$,
∴x+2y=(x+2y)($\frac{2}{x}+\frac{1}{y}$)=2+2+$\frac{4y}{x}+\frac{x}{y}$$≥4+2\sqrt{\frac{4y}{x}•\frac{x}{y}}=8$,
上式当且仅当x=2y,即x=4,y=2时等号成立.
不等式x+2y≥m2-2m恒成立,即m2-2m≤8恒成立,
解得-2≤m≤4.
∴实数m的取值范围是[-2,4].
故答案为:[-2,4].
点评 本题考查恒成立问题,考查了利用基本不等式求最值,关键是“1”的应用,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
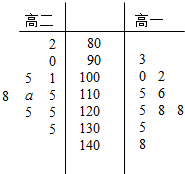 高三学生小周把自己在高二时的10次数学考试成绩和高三时的10次数学考试成绩(试卷总分150分)进行统计,统计数据用茎叶图表示(如图所示)
高三学生小周把自己在高二时的10次数学考试成绩和高三时的10次数学考试成绩(试卷总分150分)进行统计,统计数据用茎叶图表示(如图所示)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 角α和β的顶点为平面直角坐标系的原点,始边都与x轴的正半轴重合,终边分别与单位圆(半径为1)相交于点P、Q两点,已知Q点也在射线y=-$\frac{4}{3}$x(x<0)上.
角α和β的顶点为平面直角坐标系的原点,始边都与x轴的正半轴重合,终边分别与单位圆(半径为1)相交于点P、Q两点,已知Q点也在射线y=-$\frac{4}{3}$x(x<0)上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3f(2)<2f(3) | B. | 3f(3)>4f(4) | C. | 3f(4)<4f(3) | D. | f(2)<2f(1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com