
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,证明:
时,证明:![]() ;
;
(3)求证:对任意正整数![]() ,都有
,都有![]() (其中
(其中![]() ,为自然对数的底数).
,为自然对数的底数).
【答案】(1)讨论见解析;(2)证明见解析;(3)证明见解析
【解析】
(1)求出![]() ,按
,按![]() 在定义域是否恒成立分类讨论,不恒成立,求出
在定义域是否恒成立分类讨论,不恒成立,求出![]() ,
,![]() 的解,即可求出结论;
的解,即可求出结论;
(2)要证![]() ,只需证
,只需证![]() ,令
,令![]() ,只要证
,只要证![]() ,求导,求出极值最值,即可得证;
,求导,求出极值最值,即可得证;
(3)由(2)得![]() (当且仅当
(当且仅当![]() 时等号成立),令
时等号成立),令![]() ,则
,则![]() ,结合
,结合![]() ,累加再利用裂项相消法,对数运算,即可得出结论.
,累加再利用裂项相消法,对数运算,即可得出结论.
(1)函数![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
①当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,令
时,令![]() ,解得:
,解得:![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在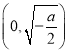 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在 上单调递增.
上单调递增.
综上,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在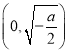 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
(2)当![]() 时,
时,![]() ,
,
要证明![]() ,即证
,即证![]() ,即
,即![]() ,
,
设![]() ,则
,则![]() ,令
,令![]() 得,
得,![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 为极大值点,也为最大值点,
为极大值点,也为最大值点,
所以![]() ,即
,即![]() ,
,
故![]() .
.
(3)由(2)得![]() (当且仅当
(当且仅当![]() 时等号成立),
时等号成立),
令![]() ,则
,则![]() ,
,
所以![]()
![]()
![]() ,
,
即![]() ,
,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】古希腊数学家阿波罗尼斯在其巨著《圆锥曲线论》中提出“在同一平面上给出三点,若其中一点到另外两点的距离之比是一个大于零且不等于1的常数,则该点轨迹是一个圆”现在,某电信公司要在甲、乙、丙三地搭建三座5G信号塔来构建一个三角形信号覆盖区域,以实现5G商用,已知甲、乙两地相距4公里,丙、甲两地距离是丙、乙两地距离的![]() 倍,则这个三角形信号覆盖区域的最大面积(单位:平方公里)是( )
倍,则这个三角形信号覆盖区域的最大面积(单位:平方公里)是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在高山滑雪运动的曲道赛项目中,运动员从高处(起点)向下滑,在滑行中运动员要穿过多个高约0.75米,宽4至6米的旗门,规定:运动员不经过任何一个旗门,都会被判一次“失格”,滑行时间会被增加,而所用时间越少,则排名越高.已知在参加比赛的运动员中,有五位运动员在滑行过程中都有三次“失格”,其中
(1)甲在滑行过程中依次没有经过![]() ,
,![]() ,
,![]() 三个旗门;
三个旗门;
(2)乙在滑行过程中依次没有经过![]() ,
,![]() ,
,![]() 三个旗门;
三个旗门;
(3)丙在滑行过程中依次没有经过![]() ,
,![]() ,
,![]() 三个旗门;
三个旗门;
(4)丁在滑行过程中依次没有经过![]() ,
,![]() ,
,![]() 三个旗门;
三个旗门;
(5)戊在滑行过程中依次没有经过![]() ,
,![]() ,
,![]() 三个旗门.
三个旗门.
根据以上信息,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这8个旗门从上至下的排列顺序共有( )种可能.
这8个旗门从上至下的排列顺序共有( )种可能.
A.6B.7C.8D.12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,侧面
中,侧面![]() 底面
底面![]() ,四边形
,四边形![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() ,
,![]() ,E,F分别为AC,
,E,F分别为AC,![]() 的中点.
的中点.

(1)求证:直线EF∥平面![]() ;
;
(2)设![]() 分别在侧棱
分别在侧棱![]() ,
,![]() 上,且
上,且![]() ,求平面BPQ分棱柱所成两部分的体积比.
,求平面BPQ分棱柱所成两部分的体积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校需从甲、乙两名学生中选一人参加物理竞赛,这两名学生最近5次的物理竞赛模拟成绩如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
学生甲的成绩(分) | 80 | 85 | 71 | 92 | 87 |
学生乙的成绩(分) | 90 | 76 | 75 | 92 | 82 |
(1)根据成绩的稳定性,现从甲、乙两名学生中选出一人参加物理竞赛,你认为选谁比较合适?
(2)若物理竞赛分为初赛和复赛,在初赛中有如下两种答题方案:方案1:每人从5道备选题中任意抽出1道,若答对,则可参加复赛,否则被淘汰;方案2:每人从5道备选题中任意抽出3道,若至少答对其中2道,则可参加复赛,否则被淘汰.若学生乙只会5道备选题中的3道,则学生乙选择哪种答题方案进入复赛的可能性更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义函数![]() 如下:对于实数
如下:对于实数![]() ,如果存在整数
,如果存在整数![]() ,使得
,使得![]() ,则
,则![]() .则下列结论:①
.则下列结论:①![]() 是实数
是实数![]() 上的递增函数;②
上的递增函数;②![]() 是周期为1的函数;③
是周期为1的函数;③![]() 是奇函数;④函数
是奇函数;④函数![]() 的图像与直线
的图像与直线![]() 有且仅有一个交点.则正确结论的序号是______.
有且仅有一个交点.则正确结论的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为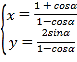 (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ),将曲线
),将曲线![]() 向左平移2个单位长度得到曲线
向左平移2个单位长度得到曲线![]() .
.
(1)求曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com