解:(1)由题函数的定义域为{x|x≠-1}
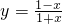
=-1+

≠-1
故函数的值域为{y|y≠-1}
(2):令

=t,t≥0,则 x=

,
∴y=
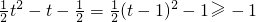
,当且仅当t=1时取等号
故所求函数的值域为[-1,+∞),
(3)原式可化为:2yx
2-3yx+y-1=0,
∴△=9y
2-8y(y-1)≥0,
∴y(y+8)≥0,
∴y>0 或y≤-8,,
故答案为:(-∞,-8]∪(0,+∞)
分析:(1)本题宜用分离常数法求值域,其定义域为{x|x≠0}函数
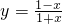
可以变为y=-1+

再由函数的单调性求值域.
(2)令

=t,将函数转化成关于t的一道定函数在定区间上的值域问题,通常利用配方法,结合函数的图象及函数在区间上的单调性,求得相应的最值,从而得函数的值域.
(3)先把函数化为:2yx
2-3yx+y-1=0,根据判别式△≥0即可得出函数的值域.
点评:本题考查了函数的值域,属于基础题,关键是掌握函数值域的两种不同求法.(1)小题求值域采用了分离常数法的技巧,对于分式形函数单调性的判断是一个好办法,注意总结这种技巧的适用范围以及使用规律.(2)是通过换元将原函数转化为某个变量的二次函数,利用二次函数的最值,确定原函数的值域.换元法是一种重要的数学解题方法,掌握它的关键在于通过观察、联想,发现与构造出变换式(或新元换旧式、或新式换旧元、或新式换旧式).

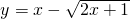
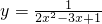 .
.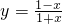 =-1+
=-1+ ≠-1
≠-1 =t,t≥0,则 x=
=t,t≥0,则 x= ,
,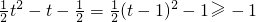 ,当且仅当t=1时取等号
,当且仅当t=1时取等号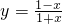 可以变为y=-1+
可以变为y=-1+ 再由函数的单调性求值域.
再由函数的单调性求值域. =t,将函数转化成关于t的一道定函数在定区间上的值域问题,通常利用配方法,结合函数的图象及函数在区间上的单调性,求得相应的最值,从而得函数的值域.
=t,将函数转化成关于t的一道定函数在定区间上的值域问题,通常利用配方法,结合函数的图象及函数在区间上的单调性,求得相应的最值,从而得函数的值域.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案