
【题目】已知![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 为其上一点,
为其上一点,![]() 与
与![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与抛物线交于异于
与抛物线交于异于![]() 的
的![]() 两点,
两点,![]() ,
,![]() .
.
(1)求抛物线的标准方程和![]() 点的坐标;
点的坐标;
(2)判断是否存在这样的直线![]() ,使得
,使得![]() 的面积最小.若存在,求出直线
的面积最小.若存在,求出直线![]() 的方程和
的方程和![]() 面积的最小值;若不存在,请说明理由.
面积的最小值;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】随着科学技术的飞速发展,手机的功能逐渐强大,很大程度上代替了电脑、电视.为了了解某高校学生平均每天使用手机的时间是否与性别有关,某调查小组随机抽取了![]() 名男生、
名男生、![]() 名女生进行为期一周的跟踪调查,调查结果如表所示:
名女生进行为期一周的跟踪调查,调查结果如表所示:
平均每天使用手机超过 | 平均每天使用手机不超过 | 合计 | |
男生 |
|
|
|
女生 |
|
|
|
合计 |
|
|
|
(1)能否在犯错误的概率不超过![]() 的前提下认为学生使用手机的时间长短与性别有关?
的前提下认为学生使用手机的时间长短与性别有关?
(2)在这![]() 名女生中,调查小组发现共有
名女生中,调查小组发现共有![]() 人使用国产手机,在这
人使用国产手机,在这![]() 人中,平均每天使用手机不超过
人中,平均每天使用手机不超过![]() 小时的共有
小时的共有![]() 人.从平均每天使用手机超过
人.从平均每天使用手机超过![]() 小时的女生中任意选取
小时的女生中任意选取![]() 人,求这
人,求这![]() 人中使用非国产手机的人数
人中使用非国产手机的人数![]() 的分布列和数学期望.
的分布列和数学期望.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: 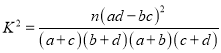
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() (
(![]() 位于第一象限)两点.
位于第一象限)两点.
(1)若直线![]() 的斜率为
的斜率为![]() ,过点
,过点![]() 分别作直线
分别作直线![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(2)若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数的极值;
垂直,求函数的极值;
(2)设函数![]() .当
.当![]() =
=![]() 时,若区间[1,e]上存在x0,使得
时,若区间[1,e]上存在x0,使得![]() ,求实数
,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数底数)
为自然对数底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以直角坐标系的原点
为参数).以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立坐标系,曲线
轴的正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且经过点
,且经过点![]() .
.
(1)求椭圆的标准方程;
(2)过点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() 两点,
两点,![]() 是
是![]() 轴上的点,若
轴上的点,若![]() 是以
是以![]() 为斜边的等腰直角三角形, 求直线
为斜边的等腰直角三角形, 求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年8月20日起,市交警支队全面启动路口秩序环境综合治理,重点整治机动车不礼让斑马线和行人的行为,经过一段时间的治理,从市交警队数据库中调取了20个路口近三个月的车辆违章数据,经统计得如图所示的频率分布直方图,统计数据中凡违章车次超过30次的设为“重点关注路口”.
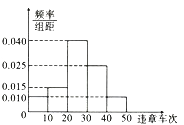
(1)现从“重点关注路口”中随机抽取两个路口安排交警去执勤,求抽出来的路口的违章车次一个在![]() ,一个在
,一个在![]() 中的概率;
中的概率;
(2)现从支队派遣5位交警,每人选择一个路口执勤,每个路口至多1人,违章车次在![]() 的路口必须有交警去,违章车次在
的路口必须有交警去,违章车次在![]() 的不需要交警过去,设去“重点关注路口”的交警人数为
的不需要交警过去,设去“重点关注路口”的交警人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com