
【题目】已知数列{an}满足al=﹣2,an+1=2an+4.
(I)证明数列{an+4}是等比数列;
(Ⅱ)求数列{|an|}的前n项和Sn .
【答案】(I)证明:∵数列{an}满足al=﹣2,an+1=2an+4,∴an+1+4=2(an+4),∴数列{an+4}是等比数列,公比与首项为2. (II)解:由(I)可得:an+4=2n , ∴an=2n﹣4,∴当n=1时,a1=﹣2;n≥2时,an≥0,
∴n≥2时,Sn=﹣a1+a2+a3+…+an=2+(22﹣4)+(23﹣4)+…+(2n﹣4)
= ![]() ﹣4(n﹣1)=2n+1﹣4n+2.n=1时也成立.
﹣4(n﹣1)=2n+1﹣4n+2.n=1时也成立.
∴Sn=2n+1﹣4n+2.n∈N* .
【解析】(I)数列{an}满足al=﹣2,an+1=2an+4,an+1+4=2(an+4),即可得出.(II)由(I)可得:an+4=2n , 可得an=2n﹣4,当n=1时,a1=﹣2;n≥2时,an≥0,可得n≥2时,Sn=﹣a1+a2+a3+…+an .


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
【题目】定义![]() 为n个正数
为n个正数![]() 的“均倒数”.已知正项数列{an}的前n项的“均倒数”为
的“均倒数”.已知正项数列{an}的前n项的“均倒数”为![]() .
.
(1)求数列{an}的通项公式.
(2)设数列![]() 的前n项和为
的前n项和为![]() ,若4
,若4![]() <
<![]() 对一切
对一切![]() 恒成立试求实数m的取值范围.
恒成立试求实数m的取值范围.
(3)令![]() ,问:是否存在正整数k使得
,问:是否存在正整数k使得![]() 对一切
对一切![]() 恒成立,如存在求出k值,否则说明理由.
恒成立,如存在求出k值,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题:
①垂直于同一条直线的两条直线平行;
②垂直于同一条直线的两个平面平行;
③垂直于同一平面的两个平面平行;
④垂直于同一平面的两条直线平行.
其中正确的命题有(填写所有正确命题的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin2x+ ![]() cos2x图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将图象上所有点向右平移
cos2x图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将图象上所有点向右平移 ![]() 个单位长度,得到函数g (x)的图象,则g(x)图象的一条对称轴方程是( )
个单位长度,得到函数g (x)的图象,则g(x)图象的一条对称轴方程是( )
A.x=一 ![]()
B.x= ![]()
C.x= ![]()
D.x= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且f(﹣x﹣1)=f(x﹣1),当x∈[﹣1,0]时,f(x)=﹣x3 , 则关于x的方程f(x)=|cosπx|在[﹣ ![]() ,
, ![]() ]上的所有实数解之和为( )
]上的所有实数解之和为( )
A.﹣7
B.﹣6
C.﹣3
D.﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,已知三角形ABC和三角形DBC所在平面互相垂直,AB=BD,∠CBA=∠CBD= ![]() ,则直线AD与平面BCD所成角的大小是( )
,则直线AD与平面BCD所成角的大小是( ) 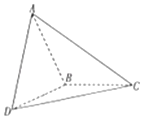
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,4),且斜率为![]() 的直线与圆C:
的直线与圆C:![]() ,相交于不同两点M、N.
,相交于不同两点M、N.
(1)求实数![]() 的取值范围;
的取值范围;
(2)求证:![]() 为定值;
为定值;
(3)若O为坐标原点,问是否存在以MN为直径的圆恰过点O,若存在则求![]() 的值,若不存在,说明理由。
的值,若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:y=k(x+2![]() )与圆O:x2+y2=4相交于不重合的A、B两点,O是坐标原点,且三点A、B、O构成三角形.
)与圆O:x2+y2=4相交于不重合的A、B两点,O是坐标原点,且三点A、B、O构成三角形.
(1)求k的取值范围;
(2)三角形ABO的面积为S,试将S表示成k的函数,并求出它的定义域;
(3)求S的最大值,并求取得最大值时k的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com