
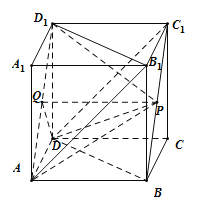
【题目】如图,在棱长为1的正方体![]() 中,P为线段
中,P为线段![]() 上的动点,下列说法正确的是( )
上的动点,下列说法正确的是( )
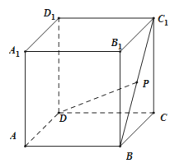
A.对任意点P,![]() 平面
平面![]()
B.三棱锥![]() 的体积为
的体积为![]()
C.线段DP长度的最小值为![]()
D.存在点P,使得DP与平面![]() 所成角的大小为
所成角的大小为![]()
【答案】ABC
【解析】
对四个选项逐一分析,
对于A:平面![]() 平面
平面![]() ,可得
,可得![]() 平面
平面![]() ;
;
对于B:三棱锥![]() 的高均为1,底面
的高均为1,底面![]() 的面积为
的面积为![]() ,根据锥体体积公式计算即可作出判断;
,根据锥体体积公式计算即可作出判断;
对于C:当点P为![]() 的中点时,DP最小,此时
的中点时,DP最小,此时![]() ,在
,在![]() 中利用勾股定理进行计算可得出DP的最小值;
中利用勾股定理进行计算可得出DP的最小值;
对于D:设点P在平面![]() 上的投影为点Q,
上的投影为点Q,![]() 为DP与平面
为DP与平面![]() 所成的角,
所成的角,![]() ,
,![]() ,而
,而![]() ,所以DP与平面
,所以DP与平面![]() 所成角的正弦值的取值范围是
所成角的正弦值的取值范围是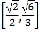 ,而
,而![]() ,从而作出判断.
,从而作出判断.
由题可知,正方体的面对角线长度为![]() ,
,
对于A:分别连接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,易得平面
,易得平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,故对任意点P,
,故对任意点P,![]() 平面
平面![]() ,故正确;
,故正确;
对于B:分别连接![]() 、
、![]() ,无论点P在哪个位置,三棱锥
,无论点P在哪个位置,三棱锥![]() 的高均为1,底面
的高均为1,底面![]() 的面积为
的面积为![]() ,所以三棱锥
,所以三棱锥![]() 的体积为
的体积为![]() ,故正确;
,故正确;
对于C:线段DP在![]() 中,当点P为
中,当点P为![]() 的中点时,DP最小,此时
的中点时,DP最小,此时![]() ,在
,在![]() 中,
中,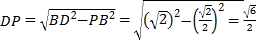 ,
,
故DP的最小值为![]() ,故正确;
,故正确;
对于D:点P在平面![]() 上的投影在线段
上的投影在线段![]() 上,设点P的投影为点Q,则
上,设点P的投影为点Q,则![]() 为DP与平面
为DP与平面![]() 所成的角,
所成的角,![]() ,
,![]() ,
,
而![]() ,所以DP与平面
,所以DP与平面![]() 所成角的正弦值的取值范围是
所成角的正弦值的取值范围是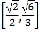 ,而
,而![]() ,
,
所以不存在点P,使得DP与平面![]() 所成角的大小为
所成角的大小为![]() ,故错误.
,故错误.
故选:ABC.


科目:高中数学 来源: 题型:
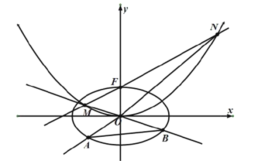
【题目】如图,已知椭圆![]() ,点
,点![]() 是抛物线
是抛物线![]() 的焦点,过点F作直线
的焦点,过点F作直线![]() 交抛物线于M,N两点,延长
交抛物线于M,N两点,延长![]() ,
,![]() 分别交椭圆于A,B两点,记
分别交椭圆于A,B两点,记![]() ,
,![]() 的面积分别是
的面积分别是![]() ,
,![]() .
.
(1)求![]() 的值及抛物线的准线方程;
的值及抛物线的准线方程;
(2)求![]() 的最小值及此时直线
的最小值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下述四个结论:
有下述四个结论:
①![]() 是偶函数;②
是偶函数;②![]() 的最大值为
的最大值为![]() ;
;
③![]() 在
在![]() 有
有![]() 个零点;④
个零点;④![]() 在区间
在区间![]() 单调递增.
单调递增.
其中所有正确结论的编号是( )
A.①②B.①③C.②④D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校拟从甲、乙两名同学中选一人参加疫情知识问答竞赛,于是抽取了甲、乙两人最近同时参加校内竞赛的十次成绩,将统计情况绘制成如图所示的折线图.根据该折线图,下面结论正确的是( )
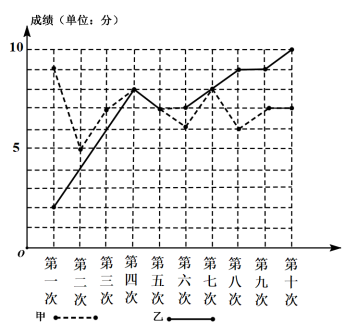
A.甲、乙成绩的中位数均为7
B.乙的成绩的平均分为6.8
C.甲从第四次到第六次成绩的下降速率要大于乙从第四次到第五次的下降速率
D.甲的成绩的方差小于乙的成绩的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对n个不同的实数a1,a2,…,an可得n!个不同的排列,每个排列为一行写成一个n!行的数阵.对第i行ai1,ai2,…,ain,记bi=-ai1+2ai2-3ai3+…+(-1)nnain,i=1,2,3…,n!.例如用1,2,3可得数阵如图,对于此数阵中每一列各数之和都是12,所以bl+b2+…b6=-12+2×12-3×12=-24.那么,在用1,2,3,4,5形成的数阵中,b1+b2+…b120等于( )

A.-3600B.-1800C.-1080D.-720
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年1月底因新型冠状病毒感染的肺炎疫情形势严峻,避免外出是减少相互交叉感染最有效的方式.在家中适当锻炼,合理休息,能够提高自身免疫力,抵抗该种病毒.某小区为了调查“宅”家居民的运动情况,从该小区随机抽取了100位成年人,记录了他们某天的锻炼时间,其频率分布直方图如下:
(1)求a的值,并估计这100位居民锻炼时间的平均值![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)小张是该小区的一位居民,他记录了自己“宅”家7天的锻炼时长:
序号n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
锻炼时长m(单位:分钟) | 10 | 15 | 12 | 20 | 30 | 25 | 35 |
(Ⅰ)根据数据求m关于n的线性回归方程;
(Ⅱ)若![]() (
(![]() 是(1)中的平均值),则当天被称为“有效运动日”.估计小张“宅”家第8天是否是“有效运动日”?
是(1)中的平均值),则当天被称为“有效运动日”.估计小张“宅”家第8天是否是“有效运动日”?
附;在线性回归方程![]() 中,
中,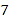 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,直线
,直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,当
两点,当![]() 时,
时,![]()
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)在椭圆![]() 上是否存在点
上是否存在点![]() ,使得当
,使得当![]() 时,
时,![]() 的平分线总是平行于
的平分线总是平行于![]() 轴?若存在,求出点
轴?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com