
【题目】小图给出了某池塘中的浮萍蔓延的面积![]() 与时间
与时间![]() (月)的关系的散点图.有以下叙述:
(月)的关系的散点图.有以下叙述:
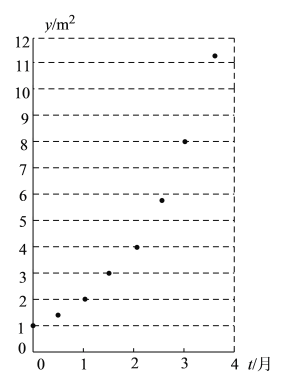
①与函数![]() 相比,函数
相比,函数![]() 作为近似刻画
作为近似刻画![]() 与
与![]() 的函数关系的模型更好;
的函数关系的模型更好;
②按图中数据显现出的趋势,第![]() 个月时,浮萍的面积就会超过
个月时,浮萍的面积就会超过![]() ;
;
③按图中数据显现出的趋势,浮萍每个月增加的面积约是上个月增加面积的两倍;
④按图中数据显现出的趋势,浮萍从![]() 月的
月的![]() 蔓延到
蔓延到![]() 至少需要经过
至少需要经过![]() 个月.
个月.
其中正确的说法有__________(填序号).
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (a>0).
(a>0).
(Ⅰ)当a=1时,求函数f(x)在点(2,f(2))处的切线方程;
(Ⅱ)求函数f(x)的单调区间;
(Ⅲ)若f(x)≥2lnx在[1,+∞)上恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 上的动点,点Q在NP上,点G在MP上,且满足
上的动点,点Q在NP上,点G在MP上,且满足![]() .
.
(I)求点G的轨迹C的方程
(II)过点(2,0)作直线![]() ,与曲线C交于A、B两点,O是坐标原点,设
,与曲线C交于A、B两点,O是坐标原点,设![]() 是否存在这样的直线
是否存在这样的直线![]() ,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线
,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线![]() 的方程若不存在,试说明理由.
的方程若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2﹣a)lnx+ ![]() +2ax(a∈R).
+2ax(a∈R).
(Ⅰ)当a=0时,求f(x)的极值;
(Ⅱ)当a<0时,求f(x)单调区间;
(Ⅲ)若对任意a∈(﹣3,﹣2)及x1 , x2∈[1,3],恒有(m+ln3)a﹣2ln3>|f(x1)﹣f(x2)|成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂每日生产一种产品![]() 吨,每日生产的产品当日销售完毕,日销售额为
吨,每日生产的产品当日销售完毕,日销售额为![]() 万元,产品价格随着产量变化而有所变化,经过一段时间的产销,得到了
万元,产品价格随着产量变化而有所变化,经过一段时间的产销,得到了![]() 的一组统计数据如下表:
的一组统计数据如下表:

(1)请判断![]() 与
与![]() 中,哪个模型更适合刻画
中,哪个模型更适合刻画![]() 之间的关系?可从函数增长趋势方面给出简单的理由;
之间的关系?可从函数增长趋势方面给出简单的理由;
(2)根据你的判断及下面的数据和公式,求出![]() 关于
关于![]() 的回归方程,并估计当日产量
的回归方程,并估计当日产量![]() 时,日销售额是多少?(结果保留整数)
时,日销售额是多少?(结果保留整数)
参考公式及数据:线性回归方程![]() 中,
中, ,
,![]() .
.
![]() ,
,![]()
![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=kcn﹣k(其中c,k为常数),且a2=4,a6=8a3 .
(1)求an;
(2)求数列{nan}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() (n∈N*)
(n∈N*)
(1)求![]() 的通项公式;
的通项公式;
(2)数列![]() 满足
满足![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() ;
;
(3)若![]() 对一切正整数n恒成立,求实数m的取值范围.
对一切正整数n恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(选修4﹣4:坐标系与参数方程)
已知直线l过点P(﹣1,2),且倾斜角为 ![]() ,圆方程为
,圆方程为 ![]() .
.
(1)求直线l的参数方程;
(2)设直线l与圆交与M、N两点,求|PM||PN|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
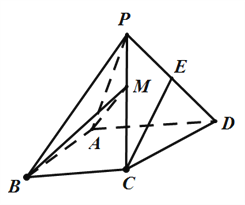
【题目】如图,四棱锥P-ABCD中,侧面PAD是边长为2的等边三角形且垂直于底![]() ,
, ![]()
![]() 是
是![]() 的中点。
的中点。
(1)证明:直线![]() 平面
平面![]() ;
;
(2)点![]() 在棱
在棱![]() 上,且直线
上,且直线![]() 与底面
与底面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的余弦值。
的余弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com