
【题目】下列各式:
(1)![]() ;
;
(2)已知![]() ,则
,则![]() ;
;
(3)函数![]() 的图象与函数
的图象与函数![]() 的图象关于y轴对称;
的图象关于y轴对称;
(4)函数![]() 的定义域是R,则m的取值范围是
的定义域是R,则m的取值范围是![]() ;
;
(5)函数![]() 的递增区间为
的递增区间为![]() .
.
正确的有______________________.(把你认为正确的序号全部写上)
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】下列说法:
①将一组数据中的每个数据都乘以同一个非零常数![]() 后,标准差也变为原来的
后,标准差也变为原来的![]() 倍;
倍;
②设有一个回归方程![]() ,变量
,变量![]() 增加1个单位时,
增加1个单位时, ![]() 平均减少5个单位;
平均减少5个单位;
③线性相关系数![]() 越大,两个变量的线性相关性越强;反之,线性相关性越弱;
越大,两个变量的线性相关性越强;反之,线性相关性越弱;
④在某项测量中,测量结果![]() 服从正态分布
服从正态分布![]() ,若
,若![]() 位于区域
位于区域![]() 的概率为0.4,则
的概率为0.4,则![]() 位于区域
位于区域![]() 内的概率为0.6
内的概率为0.6
⑤利用统计量![]() 来判断“两个事件
来判断“两个事件![]() 的关系”时,算出的
的关系”时,算出的![]() 值越大,判断“
值越大,判断“![]() 与
与![]() 有关”的把握就越大
有关”的把握就越大
其中正确的个数是
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为线段
分别为线段![]() 、
、![]() 的中点,
的中点,![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 上一点,且
上一点,且![]() ,
,![]() .
.
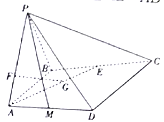
(1)确定点![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ;
;
(2)试问:直线![]() 上是否存在一点
上是否存在一点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角的大小为
所成锐二面角的大小为![]() ,若存在,求
,若存在,求![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为线段
分别为线段![]() 、
、![]() 的中点,
的中点,![]() 、
、![]() 分别为线段
分别为线段![]() 、
、![]() 上一点,且
上一点,且![]() ,
,![]() .
.

(1)确定点![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ;
;
(2)点![]() 为线段
为线段![]() 上一点,且
上一点,且![]() ,若平面
,若平面![]() 将四棱锥
将四棱锥![]() 分成体积相等的两部分,求三棱锥
分成体积相等的两部分,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
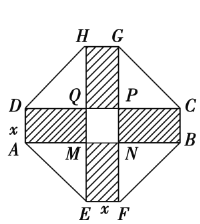
【题目】某居民小区要建造一座八边形的休闲小区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的,是面积为200平方米的十字形地带.计划在正方MNPQ上建一座花坛,造价是每平方米4 200元,在四个相同的矩形(图中阴影部分)上铺上花岗岩地坪,造价是每平方米210元,再在四个空角上铺上草坪,造价是每平方米80元.
(1)设总造价是S元,AD长为x米,试建立S关于x的函数关系式;
(2)当x为何值时,S最小?并求出最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地
区调查了500位老年人,结果如下:
男 | 女 | |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否在犯错误的概率不超过0.01的前提下认为该地区的老年人需要志愿者提供帮助与性别有
关?
附:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com