
【题目】试求下列函数的定义域与值域:
(1)f(x)=(x-1)2+1,x∈{-1,0,1,2,3};
(2)f(x)=(x-1)2+1;
(3)f(x)=![]() ;
;
(4)f(x)=x-![]() .
.
【答案】(1)详见解析;(2) 详见解析;(3) 详见解析;(4) 详见解析.
【解析】试题分析:(1)将x=-1,0,1,2,3代入解析式,求出y值,即可得函数的值域;(2) (x-1)2+1≥1,则值域为{y|y≥1};(3)分离常数,可得![]() ,因为x≠1,所以y≠5;(4)令
,因为x≠1,所以y≠5;(4)令![]() ,则x=t2-1(t≥0),代入原函数可得关于t的二次函数,通过配方法求出函数的值域.
,则x=t2-1(t≥0),代入原函数可得关于t的二次函数,通过配方法求出函数的值域.
试题解析:
(1)函数的定义域为{-1,0,1,2,3},则f(-1)=[(-1)-1]2+1=5,同理可得f(0)=2,f(1)=1,f(2)=2,f(3)=5,所以函数的值域为{1,2,5}.
(2)函数的定义域为R,因为(x-1)2+1≥1,所以函数的值域为{y|y≥1}.
(3)函数的定义域是{x|x≠1},y=![]() =5+
=5+![]() ,所以函数的值域为{y|y≠5}.
,所以函数的值域为{y|y≠5}.
(4)要使函数式有意义,需x+1≥0,即x≥-1,故函数的定义域是{x|x≥-1}.
设t=![]() ,则x=t2-1(t≥0),于是f(t)=t2-1-t=
,则x=t2-1(t≥0),于是f(t)=t2-1-t=![]() 2-
2-![]() .
.
又因为t≥0,故f(t)≥-![]() .所以函数的值域是
.所以函数的值域是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1=4,D是A1C1中点.

(1)求证:A1B∥平面B1CD;
(2)当三棱锥C-B1C1D体积最大时,求点B到平面B1CD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地方政府要将一块如图所示的直角梯形ABCD空地改建为健身娱乐广场.已知AD//BC, ![]() 百米,
百米, ![]() 百米,广场入口P在AB上,且
百米,广场入口P在AB上,且![]() ,根据规划,过点P铺设两条相互垂直的笔直小路PM,PN(小路的宽度不计),点M,N分别在边AD,BC上(包含端点),
,根据规划,过点P铺设两条相互垂直的笔直小路PM,PN(小路的宽度不计),点M,N分别在边AD,BC上(包含端点),![]() 区域拟建为跳舞健身广场,
区域拟建为跳舞健身广场, ![]() 区域拟建为儿童乐园,其它区域铺设绿化草坪,设
区域拟建为儿童乐园,其它区域铺设绿化草坪,设![]() .
.
(1)求绿化草坪面积的最大值;
(2)现拟将两条小路PNM,PN进行不同风格的美化,PM小路的美化费用为每百米1万元,PN小路的美化费用为每百米2万元,试确定M,N的位置,使得小路PM,PN的美化总费用最低,并求出最小费用.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1: ![]() (t为参数)曲线C2:
(t为参数)曲线C2:![]() +y2=4.
+y2=4.
(1)在同一平面直角坐标系中,将曲线C2上的点按坐标变换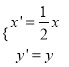 后得到曲线C′。求曲线C′的普通方程,并写出它的参数方程;
后得到曲线C′。求曲线C′的普通方程,并写出它的参数方程;
(2)若C1上的点P对应的参数为t=π/2,Q为C′上的动点,求PQ中点M到直线C3: ![]() (t为参数)的距离的最小值
(t为参数)的距离的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,AC∩BD=E,AD=2,AB=2![]() ,BC=6,求证:平面PBD⊥平面PAC.
,BC=6,求证:平面PBD⊥平面PAC.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() .若直线
.若直线![]() 与圆C相交于不同的两点P,Q.
与圆C相交于不同的两点P,Q.
(Ⅰ)写出圆C的直角坐标方程,并求圆心的坐标与半径;
(Ⅱ)若弦长|PQ|=4,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(10分)设![]() 和
和![]() 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量![]() 表示方程
表示方程
![]() 实根的个数(重根按一个计).
实根的个数(重根按一个计).
(Ⅰ)求方程![]() 有实根的概率;
有实根的概率;
(Ⅱ)求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)求在先后两次出现的点数中有5的条件下,方程![]() 有实根的概率.
有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果对任意的
,如果对任意的![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 为
为![]() 阶伸缩函数.
阶伸缩函数.
(![]() )若函数
)若函数![]() 为二阶伸缩函数,且当
为二阶伸缩函数,且当![]() 时,
时, ![]() ,求
,求![]() 的值.
的值.
(![]() )若
)若![]() 为三阶伸缩函数,且当
为三阶伸缩函数,且当![]() 时,
时, ![]() ,求证:函数
,求证:函数![]() 在
在![]() 上无零点.
上无零点.
(![]() )若函数
)若函数![]() 为
为![]() 阶伸缩函数,且当
阶伸缩函数,且当![]() 时,
时, ![]() 的取值范围是
的取值范围是![]() ,求
,求![]() 在
在![]() 上的取值范围.
上的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com