
【题目】已知椭圆E: ![]() +
+ ![]() =1的焦点在x轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.
=1的焦点在x轴上,A是E的左顶点,斜率为k(k>0)的直线交E于A,M两点,点N在E上,MA⊥NA.
(Ⅰ)当t=4,|AM|=|AN|时,求△AMN的面积;
(Ⅱ)当2|AM|=|AN|时,求k的取值范围.
【答案】【解答】解:(Ⅰ)方法一、t=4时,椭圆E的方程为 ![]() +
+ ![]() =1,A(﹣2,0),
=1,A(﹣2,0),
直线AM的方程为y=k(x+2),代入椭圆方程,整理可得(3+4k2)x2+16k2x+16k2﹣12=0,
解得x=﹣2或x=﹣ ![]() ,则|AM|=
,则|AM|= ![]() |2﹣
|2﹣ ![]() |=
|= ![]()
![]() ,
,
由AN⊥AM,可得|AN|= ![]()
![]() =
= ![]()
![]() ,
,
由|AM|=|AN|,k>0,可得 ![]()
![]() =
= ![]()
![]() ,
,
整理可得(k﹣1)(4k2+k+4)=0,由4k2+k+4=0无实根,可得k=1,
即有△AMN的面积为 ![]() |AM|2=
|AM|2= ![]() (
( ![]()
![]() )2=
)2= ![]() ;
;
方法二、由|AM|=|AN|,可得M,N关于x轴对称,
由MA⊥NA.可得直线AM的斜率为1,直线AM的方程为y=x+2,
代入椭圆方程 ![]() +
+ ![]() =1,可得7x2+16x+4=0,
=1,可得7x2+16x+4=0,
解得x=﹣2或﹣ ![]() ,M(﹣
,M(﹣ ![]() ,
, ![]() ),N(﹣
),N(﹣ ![]() ,﹣
,﹣ ![]() ),
),
则△AMN的面积为 ![]() ×
× ![]() ×(﹣
×(﹣ ![]() +2)=
+2)= ![]() ;
;
(Ⅱ)直线AM的方程为y=k(x+ ![]() ),代入椭圆方程,
),代入椭圆方程,
可得(3+tk2)x2+2t ![]() k2x+t2k2﹣3t=0,
k2x+t2k2﹣3t=0,
解得x=﹣ ![]() 或x=﹣
或x=﹣ ![]() ,
,
即有|AM|= ![]() |
| ![]() ﹣
﹣ ![]() |=
|= ![]()
![]() ,
,
|AN|═ ![]()
![]() =
= ![]()
![]() ,
,
由2|AM|=|AN|,可得2 ![]()
![]() =
= ![]()
![]() ,
,
整理得t= ![]() ,
,
由椭圆的焦点在x轴上,则t>3,即有 ![]() >3,即有
>3,即有 ![]() <0,
<0,
可得 ![]() <k<2,即k的取值范围是(
<k<2,即k的取值范围是( ![]() ,2).
,2).
【解析】(1)法一:当t=4时,椭圆方程和顶点坐标确定。设直线AM的方程为y=k(x+2),代入椭圆方程联立方程组接得x的值。又由|AM|=|AN|=![]() 整理可得k=1,所以
整理可得k=1,所以![]() 。法二:运用椭圆的对称性得到直线AM的斜率为1,将直线AM的方程代入椭圆方程,得到M,N点坐标,即可求三角形的面积。
。法二:运用椭圆的对称性得到直线AM的斜率为1,将直线AM的方程代入椭圆方程,得到M,N点坐标,即可求三角形的面积。
(2)直线AM的方程为y=k(x+![]() ),代入椭圆方程得到x的值。即可得|AM|,|AN|。又由2|AM|=|AN|,可得t。结合椭圆得到k的范围。
),代入椭圆方程得到x的值。即可得|AM|,|AN|。又由2|AM|=|AN|,可得t。结合椭圆得到k的范围。


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.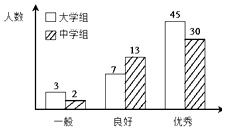
(Ⅰ)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的2×2列联表,并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?
优秀 | 合格 | 合计 | |
大学组 | |||
中学组 | |||
合计 |
注:K2 ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
P(k2≥k0) | 0.10 | 0.05 | 0.005 |
k0 | 2.706 | 3.841 | 7.879 |
(Ⅱ)若江西参赛选手共80人,用频率估计概率,试估计其中优秀等级的选手人数;
(Ⅲ)如果在优秀等级的选手中取4名,在良好等级的选手中取2名,再从这6人中任选3人组成一个比赛团队,求所选团队中的有2名选手的等级为优秀的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,△PAD为正三角形,平面PAD⊥平面ABCD,E为AD的中点,AB∥CD,AB⊥AD,CD=2AB=2AD=4.
(Ⅰ)求证:平面PCD⊥平面PAD;
(Ⅱ)求直线PB与平面PCD所成角的正弦值;
(Ⅲ)在棱CD上是否存在点M,使得AM⊥平面PBE?若存在,求出 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车是指企业在校园、地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车单车共享服务,是共享经济的一种新形态.一个共享单车企业在某个城市就“一天中一辆单车的平均成本(单位:元)与租用单车的数量(单位:千辆)之间的关系”进行调查研究,在调查过程中进行了统计,得出相关数据见下表:
租用单车数量x(千辆) | 2 | 3 | 4 | 5 | 8 |
每天一辆车平均成本y(元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
根据以上数据,研究人员分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲: ![]() (1)=
(1)= ![]() +1.1,方程乙:
+1.1,方程乙: ![]() (2)=
(2)= ![]() +1.6.
+1.6.
(1)为了评价两种模型的拟合效果,完成以下任务:
①完成下表(计算结果精确到0.1)(备注: ![]() =yi﹣
=yi﹣ ![]() ,
, ![]() 称为相应于点(xi , yi)的残差(也叫随机误差);
称为相应于点(xi , yi)的残差(也叫随机误差);
租用单车数量x(千辆) | 2 | 3 | 4 | 5 | 8 | |
每天一辆车平均成本y(元) | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
模型甲 | 估计值 | 2.4 | 2.1 | 1.6 | ||
残差 | 0 | ﹣0.1 | 0.1 | |||
模型乙 | 估计值 | 2.3 | 2 | 1.9 | ||
残差 | 0.1 | 0 | 0 | |||
②分别计算模型甲与模型乙的残差平方和Q1及Q2 , 并通过比较Q1 , Q2的大小,判断哪个模型拟合效果更好.
(2)这个公司在该城市投放共享单车后,受到广大市民的热烈欢迎,共享单车常常供不应求,于是该公司研究是否增加投放.根据市场调查,这个城市投放8千辆时,该公司平均一辆单车一天能收入10元,6元收入的概率分别为0.6,0.4;投放1万辆时,该公司平均一辆单车一天能收入10元,6元的概率分别为0.4,0.6.问该公司应该投放8千辆还是1万辆能获得更多利润?(按(1)中拟合效果较好的模型计算一天中一辆单车的平均成本,利润=收入﹣成本).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xoy中,抛物线C的顶点在原点,以x轴为对称轴,且经过点P(1,2).设点A,B在抛物线C上,直线PA,PB分别与y轴交于点M,N,|PM|=|PN|,则直线AB的斜率大小是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若ax2+bx+c<0的解集为{x|x<-2,或x>4},则对于函数f(x)=ax2+bx+c应有( )
A.f(5)<f(2)<f(-1)
B.f(5)<f(-1)<f(2)
C.f(-1)<f(2)<f(5)
D.f(2)<f(-1)<f(5)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系 ![]() 中,点
中,点 ![]() 在抛物线
在抛物线 ![]() 上.
上.
(1)求 ![]() 的方程和
的方程和 ![]() 的焦点的坐标;
的焦点的坐标;
(2)设点 ![]() 为准线与
为准线与 ![]() 轴的交点,直线
轴的交点,直线 ![]() 过点
过点 ![]() ,且与直线
,且与直线 ![]() 垂直,求证:
垂直,求证: ![]() 与
与 ![]() 相切.
相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com