
| A. | $\frac{33}{8}$ | B. | 6 | C. | 5 | D. | $\frac{69}{17}$ |
分析 根据等差数列的前n项和的性质,可得${S}_{15}=\frac{{15(a}_{1}+{a}_{15})}{2}$=$\frac{15×2{a}_{8}}{2}$,${T}_{15}=\frac{15({b}_{1}+{b}_{15})}{2}$=$\frac{15×2{b}_{8}}{2}$,可得答案.
解答 解:根据等差数列的前n项和的性质,可得${S}_{15}=\frac{{15(a}_{1}+{a}_{15})}{2}$=$\frac{15×2{a}_{8}}{2}$,${T}_{15}=\frac{15({b}_{1}+{b}_{15})}{2}$=$\frac{15×2{b}_{8}}{2}$,
那么$\frac{{S}_{15}}{{T}_{15}}$=$\frac{{a}_{8}}{{b}_{8}}$=$\frac{3×8+21}{8+1}$=5.
故选C
点评 本题考查了等差数列的前n项和的性质的运用.属于基础题.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 老年人应作为重点调查对象,故抽取的老年人应超过40名 | |
| B. | 每个人被抽到的概率相同为$\frac{1}{10}$ | |
| C. | 应使用分层抽样抽取样本调查 | |
| D. | 抽出的样本能在一定程度上反映总体的健康状况 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①④ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | 12 | D. | -12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
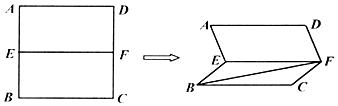 如图,已知E,F分别是正方形ABCD的边AB、CD的中点,现将正方形沿EF折成60°的二面角,则异面角直线AE与BF所成角的余弦值是$\frac{\sqrt{5}}{10}$.
如图,已知E,F分别是正方形ABCD的边AB、CD的中点,现将正方形沿EF折成60°的二面角,则异面角直线AE与BF所成角的余弦值是$\frac{\sqrt{5}}{10}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com