
已知函数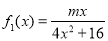 ,
,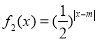 ,其中m∈R.
,其中m∈R.
(1)若0<m≤2,试判断函数f (x)=f1 (x)+f2 (x)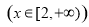 的单调性,并证明你的结论;
的单调性,并证明你的结论;
(2)设函数 若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得g (x1) = g (x2) 成立,试确定实数m的取值范围.
若对任意大于等于2的实数x1,总存在唯一的小于2的实数x2,使得g (x1) = g (x2) 成立,试确定实数m的取值范围.
(1)单调减函数,(2)(0,4).
【解析】
试题分析:(1)两个函数独立,可分别论证函数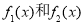 在
在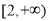 上单调递减,再得函数f(x)为单调减函数.因为
上单调递减,再得函数f(x)为单调减函数.因为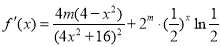 ,所以当0<m≤2,x≥2时,
,所以当0<m≤2,x≥2时,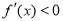 ,从而函数f(x)为单调减函数.(2)结合图形分析,可知讨论点为
,从而函数f(x)为单调减函数.(2)结合图形分析,可知讨论点为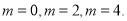 当 m≤0时
当 m≤0时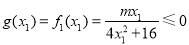 ,
,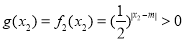 ,所以g (x1) = g (x2)不成立.当0<m<2时,
,所以g (x1) = g (x2)不成立.当0<m<2时,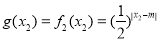 ,
, ,
, ,
,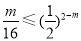 ,所以g (x1) = g (x2)恒成立.当2≤m<4时,
,所以g (x1) = g (x2)恒成立.当2≤m<4时,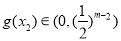 ,
,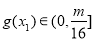 ,
,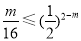 ,所以g (x1) = g (x2)恒成立.当m≥4时,
,所以g (x1) = g (x2)恒成立.当m≥4时,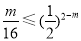 不成立.
不成立.
【解析】
(1)f (x)为单调减函数.
证明:由0<m≤2,x≥2,可得
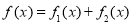 =
=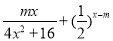 =
=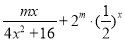 .
.
由 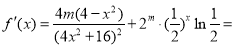
 ,
,
且0<m≤2,x≥2,所以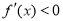 .从而函数f(x)为单调减函数.
.从而函数f(x)为单调减函数.
(亦可先分别用定义法或导数法论证函数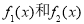 在
在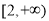 上单调递减,再得函数f(x)为单调减函数.)
上单调递减,再得函数f(x)为单调减函数.)
(2)①若m≤0,由x1≥2,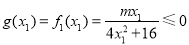 ,
,
x2<2,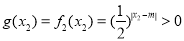 ,
,
所以g (x1) = g (x2)不成立.
②若m>0,由x>2时,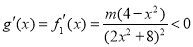 ,
,
所以g(x)在 单调递减.从而
单调递减.从而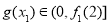 ,即
,即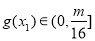 .
.
(a)若m≥2,由于x<2时, ,
,
所以g(x)在(-∞,2)上单调递增,从而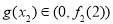 ,即
,即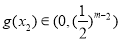 .
.
要使g (x1) = g (x2)成立,只需 ,即
,即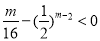 成立即可.
成立即可.
由于函数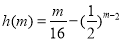 在
在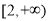 的单调递增,且h(4)=0,
的单调递增,且h(4)=0,
所以2≤m<4.
(b)若0<m<2,由于x<2时,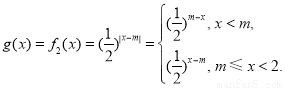
所以g(x)在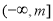 上单调递增,在
上单调递增,在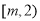 上单调递减.
上单调递减.
从而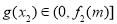 ,即
,即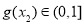 .
.
要使g (x1) = g (x2)成立,只需 成立,即
成立,即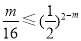 成立即可.
成立即可.
由0<m<2,得 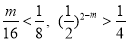 .
.
故当0<m<2时,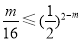 恒成立.
恒成立.
综上所述,m为区间(0,4)上任意实数.
考点:利用导数研究函数单调性,利用导数求参数取值范围


科目:高中数学 来源:2013-2014学年江苏省高三下学期4月周练文科数学试卷(解析版) 题型:解答题
已知函数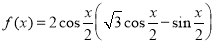 .
.
(1)设 ,且
,且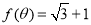 ,求
,求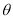 的值;
的值;
(2)在△ABC中,AB=1,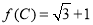 ,且△ABC的面积为
,且△ABC的面积为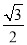 ,求sinA+sinB的值.
,求sinA+sinB的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高三下学期4月周练文科数学试卷(解析版) 题型:填空题
将函数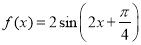 的图像向右平移
的图像向右平移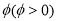 个单位,再将图像上每一点横坐标缩短到原来的
个单位,再将图像上每一点横坐标缩短到原来的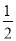 倍,所得图像关于直线
倍,所得图像关于直线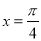 对称,则
对称,则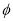 的最小正值为 .
的最小正值为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省徐州市高三第三次质量检测理科数学试卷(解析版) 题型:解答题
如图,在五面体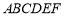 中,已知
中,已知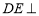 平面
平面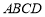 ,
,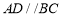 ,
,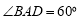 ,
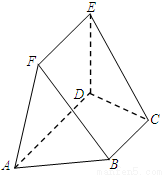
,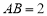 ,
, .
.
(1)求证: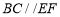 ;
;
(2)求三棱锥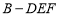 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com