【答案】
分析:(1)先设出过P的切线方程,与抛物线方程联立,因为切线与抛物线只可能有一个交点,所以∴△=0,就可求出两条切线的斜率之积,再用导数求出曲线在A,B点的切线斜率,用A,B点的横坐标表示,就可得到A,B点的横坐标的关系式,因为M时A,B的中点,把M点坐标用A,B点坐标表示,代入前面求出的A,B横坐标满足的关系式,消去参数,就可得到M点的轨迹方程.
(2)利用导数,求出曲线在A,B点的切线斜率,把两条切线方程都用以A,B点坐标为参数的方程表示,观察两个方程,形式相同,都满足y=2tx+2,所以可得到直线AB的方程为y=2tx+2.
(3)用点到直线的距离公式求出三角形PAB的高,用弦长公式求出线段AB长,代入
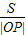
,化简为直含t的式子,再用导数求出最小值.
解答:解:(1)设过P(t,0)与抛物线y=x
2+1的相切的直线的斜率是k,
则该切线的方程为:y=k(x-t)
由

,得,x
2-kx+(kt+1)=0
∵直线与抛物线相切,
∴方程x
2-kx+(kt+1)=0有一解,
∴△=k
2-4(kt+1)=k
2-4tk-4=0
则k
1,k
2都是方程k
2-4tk-4=0的解,故k
1k
2=-4
设A(x
1,y
1),B(x
2,y
2),M(x,y)
对函数y=x
2+1求导数,得y′=2x,
∴抛物线y=x
2+1在A(x
1,y
1)点处的切线斜率为2x
1,在B(x
2,y
2)点处的切线斜率为2x
2,
∴2x
1•2x
2=-4,即x
1x
2=-1
∵M为AB中点,∴x=
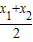
,y=
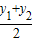
∵A,B点在抛物线y=x
2+1,∴y
1=x
12+1,y
2=x
22+1,
∴y
1+y
2=x
12+1+x
22+1=(x
1+x
2)
2-2x
1x
2+2
即2y=(2x)
2+2+2,2x
2-y+2=0
∴线段AB中点M的轨迹方程为2x
2-y+2=0
(2)由(1)知,直线PA的方程为y-y
1=2x
1(x-x
1),直线PB的方程为y-y
2=2x
2(x-x
2),
∵P(t,0)为两条切线的交点,∴-y
1=2x
1(t-x
1),即-y
1=2x
1t-2x
12,
∵y
1=x
12+1,∴-y
1=2x
1t-2(y
1-1),y
1=2x
1t+2,同理,y
2=2x
2t+2,
∴直线AB的方程是y=2tx+2,则直线PQ过定点(0,2).
(3)P点到AB的距离d=
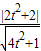
=
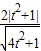
联立直线AB与抛物线y=x
2+1,
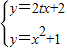
消去y,得,x
2-2tx-1=0
∴x
1+x
2=2t,x
1x
2=-1,∴|AB|=

|x
1-x
2|=
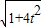

=
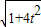
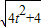
|OP|=|t|
∴
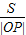
=
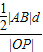
=

=

=2

(t≠0)
令
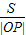
=m,则m=

对m求导,的m′=
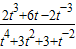
,令m′=0,得,t=-

,
∵当t<0时,m′<0.t>0时,m′>0,∴函数m=

在t=-
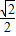
处有极小值,
又∵函数在整个定义域上只有一个极小值,
∴此时函数有最小值,也即

有最小值,最小值为
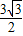
.
点评:本题主要考查直线与抛物线相切位置关系的判断,导数与曲线的切线斜率之间的关系,以及应用导数求函数的最小值.

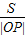 的最小值.
的最小值.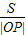 ,化简为直含t的式子,再用导数求出最小值.
,化简为直含t的式子,再用导数求出最小值. ,得,x2-kx+(kt+1)=0
,得,x2-kx+(kt+1)=0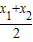 ,y=
,y=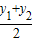
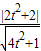 =
=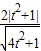
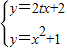 消去y,得,x2-2tx-1=0
消去y,得,x2-2tx-1=0 |x1-x2|=
|x1-x2|=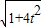
 =
=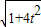
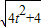
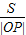 =
=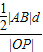 =
= =
= =2
=2 (t≠0)
(t≠0)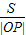 =m,则m=
=m,则m=
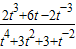 ,令m′=0,得,t=-
,令m′=0,得,t=- ,
, 在t=-
在t=-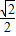 处有极小值,
处有极小值, 有最小值,最小值为
有最小值,最小值为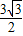 .
.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案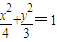 的中心,且焦点与该椭圆右焦点重合.
的中心,且焦点与该椭圆右焦点重合.