
【题目】某市医疗保险实行定点医疗制度,按照“就近就医、方便管理” 的原则,规定参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为就诊的医疗机构.若甲、乙、丙、丁4名参加保险人员所在地区附近有![]() 三家社区医院,并且他们的选择是等可能的、相互独立的.
三家社区医院,并且他们的选择是等可能的、相互独立的.
(1)求甲、乙两人都选择![]() 社区医院的概率;
社区医院的概率;
(2)求甲、乙两人不选择同一家社区医院的概率;
(3)设在4名参加保险人员中选择![]() 社区医院的人数为
社区医院的人数为![]() ,求
,求![]() 的分布列和数学期望及方差.
的分布列和数学期望及方差.
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)答案见解析.
;(3)答案见解析.
【解析】试题分析:(1)设“甲、乙两人都选择A社区医院”为事件A,由于他们的选择是相互独立,故利用乘法公式可求;
(2)先求甲、乙两人选择同一个社区医院的事件的概率,再求甲、乙两人不选择同一个社区医院的概率;
(3)确定随机变量ξ可能取的值,计算相应的概率,即可得到ξ的分布列和数学期望及方差.
试题解析:
(1)设“甲、乙两人都选择A社区医院”为事件A,那么
P(A)=![]() ×
×![]() =
=![]() ,
,
所以甲、乙两人都选择A社区医院的概率为![]() .
.
(2)设“甲、乙两人选择同一家社区医院”为事件B,那么
P(B)=C×![]() ×
×![]() =
=![]() ,
,
所以甲、乙两人不选择同一家社区医院的概率
P(![]() )=1-P(B)=
)=1-P(B)=![]() .
.
依题意ξ~B(4,![]() ),
),
所以P(ξ=k)=C×(![]() )k×(
)k×(![]() )4-k=C×
)4-k=C×![]() .
.
故ξ的分布列为
ξ | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
所以ξ的数学期望E(ξ)=4×![]() =
=![]() .
.
方差D(ξ)=4×![]() ×(1-
×(1-![]() )=
)=![]()


科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边长分别为a,b,c,且cos2B﹣cos2A=2sinC(sinA﹣sinC).
(1)求角B的大小;
(2)若 ![]() ,求2a+c的取值范围.
,求2a+c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 内一点
内一点![]() ,直线
,直线![]() 过点
过点![]() 且与圆
且与圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)求圆![]() 的圆心坐标和面积;
的圆心坐标和面积;
(2)若直线![]() 的斜率为
的斜率为![]() ,求弦
,求弦![]() 的长;
的长;
(3)若圆上恰有三点到直线![]() 的距离等于
的距离等于![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]()
(1)若![]() ,过点
,过点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若曲线![]() 表示圆时,已知圆
表示圆时,已知圆![]() 与圆
与圆![]() 交于
交于![]() 两点,若弦
两点,若弦![]() 所在的直线方程为
所在的直线方程为![]() ,
, ![]() 为圆
为圆![]() 的直径,且圆
的直径,且圆![]() 过原点,求实数
过原点,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
如图在直三棱柱ABC—A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的
中点.
(1) 求证: AC⊥BC1
(2) 求证:AC1∥平面CDB1
(3) 求异面直线AC1与B1C所成角的余弦值.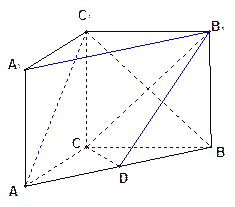
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市电视台为了宣传举办问答活动,随机对该市15~65岁的人群抽样了![]() 人,回答问题计结果如下图表所示:
人,回答问题计结果如下图表所示:

(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,则第2,3,4组每组各抽取多少人?
(3)在(2)的前提下,电视台决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com