
【题目】已知函数f(x)=x2+bx+1满足f(1+x)=f(1﹣x), ![]() .
.
(1)求函数f(x)的解析式;
(2)判断g(x)在[1,2]上的单调性并用定义证明你的结论;
(3)求g(x)在[1,2]上的最大值和最小值.
【答案】
(1)解:函数f(x)=x2+bx+1满足f(1+x)=f(1﹣x),
可知函数的对称轴为:x=1,所以 ![]() ,b=﹣2,
,b=﹣2,
函数f(x)的解析式:f(x)=x2﹣2x+1
(2)解: ![]() =x+
=x+ ![]() ﹣2,g(x)在[1,2]上的单调性是增函数,
﹣2,g(x)在[1,2]上的单调性是增函数,
证明:设1≤x1<x2≤2,x1﹣x2<0, ![]() >0,
>0,
g(x1)﹣g(x2)=x1﹣x2+ ![]() =(x1﹣x2)(
=(x1﹣x2)( ![]() )<0,
)<0,
g(x1)<g(x2),
所以函数g(x)在[1,2]上是增函数
(3)解:由(2)可知,函数是增函数,函数的最小值为:g(1)=0,
函数的最大值为:g(2)= ![]()
【解析】(1)利用二次函数的对称性求出b,然后求解函数的解析式.(2)判断函数的单调性,利用单调性的定义证明即可.(3)利用函数的单调性,直接求解函数的最值即可.
【考点精析】本题主要考查了函数的最值及其几何意义和二次函数的性质的相关知识点,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值;当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减才能正确解答此题.
上递减才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某地教育研究中心为了调查该地师生对“高考使用全国统一命题的试卷”这一看法,对该市区部分师生进行调查,先将调查结果统计如下:
赞成 | 反对 | 总计 | |
教师 | 120 | ||
学生 | 40 | ||
总计 | 280 | 120 |
(1)请将表格补充完整,若该地区共有教师30000人,以频率为概率,试估计该地区教师反对“高考使用全国统一命题的试卷”这一看法的人数;
(2)按照分层抽样从“反对”的人中先抽取6人,再从中随机选出3人进行深入调研,求深入调研中恰有1名学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若f(x)为二次函数,﹣1和3是方程f(x)﹣x﹣4=0的两根,f(0)=1
(1)求f(x)的解析式;
(2)若在区间[﹣1,1]上,不等式f(x)>2x+m有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学家通过研究学生的学习行为发现;学生的接受能力与老师引入概念和描述问题所用的时间相关,教学开始时,学生的兴趣激增,学生的兴趣保持一段较理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用f(x)表示学生掌握和接受概念的能力,x表示讲授概念的时间(单位:min),可有以下的关系:f(x)= 
(Ⅰ)开讲后第5min与开讲后第20min比较,学生的接受能力何时更强一些?
(Ⅱ)开讲后多少min学生的接受能力最强?能维持多少时间?
(Ⅲ)若一个新数学概念需要55以上(包括55)的接受能力以及13min时间,那么老师能否在学生一直达到所需接受能力的状态下讲授完这个概念?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比,已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图). 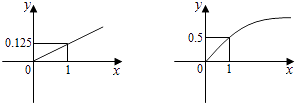
(1)分别写出两种产品的收益和投资的函数关系;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎样分配资金能使投资获得最大的收益,其最大收益为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() (其中
(其中![]() 为常数,
为常数, ![]() 为自然对数的底数),曲线
为自然对数的底数),曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行.
轴平行.
(1)求![]() 的单调区间;
的单调区间;
(2)当![]() 时,若函数
时,若函数![]() 有两个不同零点,求实数
有两个不同零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com