
【题目】已知函数 ![]() ,
, ![]() ,实数
,实数 ![]() ,
, ![]() 满足
满足 ![]() ,若
,若 ![]() ,
, ![]() ,使得
,使得 ![]() 成立,则
成立,则 ![]() 的最大值为( )
的最大值为( )
A.4
B.![]()
C.![]()
D.3
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (
( ![]() 为实常数).
为实常数).
(1)若 ![]() ,
, ![]() ,求
,求 ![]() 的单调区间;
的单调区间;
(2)若 ![]() ,且
,且 ![]() ,求函数
,求函数 ![]() 在
在 ![]() 上的最小值及相应的
上的最小值及相应的 ![]() 值;
值;
(3)设 ![]() ,若存在
,若存在 ![]() ,使得
,使得 ![]() 成立,求实数
成立,求实数 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|,其中a>1
(1)当a=2时,求不等式f(x)≥4﹣|x﹣4|的解集;
(2)已知关于x的不等式|f(2x+a)﹣2f(x)|≤2的解集{x|1≤x≤2},求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠ABC=∠BAD=90°,![]() ,
,![]() ,F分别为AB,PC的中点.
,F分别为AB,PC的中点.
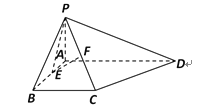
(I)若四棱锥P-ABCD的体积为4,求PA的长;
(II)求证:PE⊥BC;
(III)求PC与平面PAD所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是由正整数构成的数表,用aij表示i行第j个数(i,j∈N+).此表中ail=aii=i,每行中除首尾两数外,其他各数分别等于其“肩膀”上的两数之和.

(1)写出数表的第六行(从左至右依次列出).
(2)设第n行的第二个数为bn(n≥2),求bn.
(3)令![]() ,记Tn为数列
,记Tn为数列![]() 前n项和,求
前n项和,求![]() 的最大值,并求此时n的值.
的最大值,并求此时n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小朋友按如下规则练习数数,![]() 大拇指,
大拇指,![]() 食指,
食指,![]() 中指,
中指,![]() 无名指,
无名指,![]() 小指,
小指,![]() 无名指,
无名指,![]() 中指,
中指,![]() 食指,
食指,![]() 大拇指,
大拇指,![]() 食指,
食指,![]() ,一直数到
,一直数到![]() 时,对应的指头是( )
时,对应的指头是( )

A. 小指 B. 中指 C. 食指 D. 无名指
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com