【题目】从向阳小区抽取100户居民进行月用电量调查，为制定阶梯电价提供数据，发现其用电量都在50到350度之间，制作频率分布直方图的工作人员粗心大意，位置t处未标明数据，你认为t=（ ） 
A.0.0041
B.0.0042
C.0.0043
D.0.0044
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
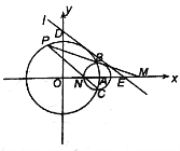
【题目】在平面直角坐标系中，圆
： 
与
轴的正半轴交于点
，以
为圆心的圆
： 
（
）与圆
交于
， 
两点.
（1）若直线
与圆
切于第一象限，且与坐标轴交于
， 
，当直线
长最小时，求直线
的方程；
（2）设
是圆
上异于
， 
的任意一点，直线
、
分别与
轴交于点
和
，问
是否为定值？若是，请求出该定值；若不是，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
且
，函数
.
（1）求
的定义域
及其零点；
（2）讨论并用函数单调性定义证明函数
在定义域
上的单调性；
（3）设
，当
时，若对任意
，存在
，使得
，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在如图所示的几何体中，平面
平面
，四边形是菱形，四边形
是矩形，
，
，
，
是
的中点．
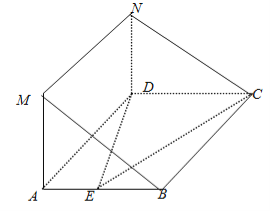
(Ⅰ)求证：
平面
；
(II)在线段
上是否存在一点
，使三棱锥
的体积为
？若存在，求出
的长；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列关于回归分析的说法中错误的是（ ）
A. 回归直线一定过样本中心
B. 残差图中残差点比较均匀地落在水平的带状区域中，说明选用的模型比较合适
C. 两个模型中残差平方和越小的模型拟合的效果越好
D. 甲、乙两个模型的
分别约为0.98和0.80，则模型乙的拟合效果更好
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知曲线
的极坐标方程是
，以极点为平面直角坐标系的原点，极轴为
轴的正半轴，建立平面直角坐标系，在平面直角坐标系
中，直线
经过点
，倾斜角
.
（1）写出曲线
的直角坐标方程和直线
的参数方程；
（2）设
与曲线
相交于
， 
两点，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，且 
（a﹣ccosB）=bsinC．
（1）求角C的大小；
（2）若c=2，则当a，b分别取何值时，△ABC的面积取得最大值，并求出其最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一台机器使用时间较长，但还可以使用．它按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少，随机器运转的速度而变化，如表为抽样试验结果：
转速x（转/秒） | 16 | 14 | 12 | 8 |
每小时生产有 缺点的零件数y（件） | 11 | 9 | 8 | 5 |
（1）用相关系数r对变量y与x进行相关性检验；
（2）如果y与x有线性相关关系，求线性回归方程；
（3）若实际生产中，允许每小时的产品中有缺点的零件最多为10个，那么，机器的运转速度应控制在什么范围内？（结果保留整数）
参考数据：
，
，
．
参考公式：相关系数计算公式：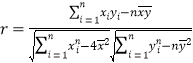
,回归方程
中斜率和截距的最小二乘估计公式分别为：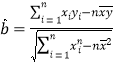
，
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
