
【题目】已知![]() ,
,![]() ,其中
,其中![]() ,则下列判断正确的是__________.(写出所有正确结论的序号)
,则下列判断正确的是__________.(写出所有正确结论的序号)
①![]() 关于点
关于点![]() 成中心对称;
成中心对称;
②![]() 在
在![]() 上单调递增;
上单调递增;
③存在![]() ,使
,使![]() ;
;
④若![]() 有零点,则
有零点,则![]() ;
;
⑤![]() 的解集可能为
的解集可能为![]() .
.
【答案】①③⑤
【解析】
对于①,根据函数![]() 为奇函数并结合函数图象的平移可得正确.对于②,分析可得当
为奇函数并结合函数图象的平移可得正确.对于②,分析可得当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,故不正确.对于③,由
上单调递减,故不正确.对于③,由![]() ,可得
,可得![]() ,从而得
,从而得![]()
![]() ,可得结果成立.对于④,根据③中的函数的值域可得
,可得结果成立.对于④,根据③中的函数的值域可得![]() 时方程也有解.对于⑤,分析可得当
时方程也有解.对于⑤,分析可得当![]() 时满足条件,由此可得⑤正确.
时满足条件,由此可得⑤正确.
对于①,令![]() ,则该函数的定义域为
,则该函数的定义域为![]() ,且函数为奇函数,故其图象关于原点
,且函数为奇函数,故其图象关于原点![]() 对称.又函数
对称.又函数![]() 的图象是由
的图象是由![]() 的图象向上或向下平移
的图象向上或向下平移![]() 个单位而得到的,所以函数
个单位而得到的,所以函数![]() 图象的对称中心为
图象的对称中心为![]() ,故①正确.
,故①正确.
对于②,当![]() 时,
时,![]() ,若
,若![]() ,则函数
,则函数![]() 在
在![]() 上单调递减,所以函数
上单调递减,所以函数![]() 单调递增;函数
单调递增;函数![]() 在
在![]() 上单调递增,所以函数
上单调递增,所以函数![]() 单调递减.故②不正确.
单调递减.故②不正确.
对于③,令![]() ,则当
,则当![]() 时,
时,![]() ,
,
则![]() .
.
所以![]() ,
,
令![]() ,则
,则![]() 成立.故③正确.
成立.故③正确.
对于④,若![]() 有零点,则
有零点,则![]() ,得
,得![]() ,从而得
,从而得![]() ,
,
故![]() ,结合③可得当
,结合③可得当![]() 有零点时,只需
有零点时,只需![]() 即可,而
即可,而![]() 不一定为零.故④不正确.
不一定为零.故④不正确.
对于⑤,由![]() ,得
,得![]() .取
.取![]() ,则
,则![]() ,整理得
,整理得![]() .当
.当![]() 时,方程
时,方程![]() 的两根为
的两根为![]() 或
或![]() .又函数
.又函数![]() 为奇函数,故方程的解集为
为奇函数,故方程的解集为![]() .故⑤正确.
.故⑤正确.
综上可得①③⑤正确.
故答案为:①③⑤


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】2019年春节期间,我国高速公路继续执行“节假日高速公路免费政策”某路桥公司为掌握春节期间车辆出行的高峰情况,在某高速公路收费点记录了大年初三上午9:20~10:40这一时间段内通过的车辆数,统计发现这一时间段内共有600辆车通过该收费点,它们通过该收费点的时刻的频率分布直方图如下图所示,其中时间段9:20~9:40记作区间![]() ,9:40~10:00记作
,9:40~10:00记作![]() ,10:00~10:20记作
,10:00~10:20记作![]() ,10:20~10:40记作
,10:20~10:40记作![]() .例如:10点04分,记作时刻64.
.例如:10点04分,记作时刻64.

(1)估计这600辆车在9:20~10:40时间段内通过该收费点的时刻的平均值(同一组中的数据用该组区间的中点值代表);
(2)为了对数据进行分析,现采用分层抽样的方法从这600辆车中抽取10辆,再从这10辆车中随机抽取4辆,设抽到的4辆车中,在9:20~10:00之间通过的车辆数为X,求X的分布列与数学期望;
(3)由大数据分析可知,车辆在每天通过该收费点的时刻T服从正态分布![]() ,其中
,其中![]() 可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,
可用这600辆车在9:20~10:40之间通过该收费点的时刻的平均值近似代替,![]() 可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
可用样本的方差近似代替(同一组中的数据用该组区间的中点值代表),已知大年初五全天共有1000辆车通过该收费点,估计在9:46~10:40之间通过的车辆数(结果保留到整数).
参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x),若a,b,c∈R,f(a),f(b),f(c)为某一三角形的三边长,则称f(x)为“可构造三角形函数”.已知函数f(x)=![]() 是“可构造三角形函数”,则实数t的取值范围是( )
是“可构造三角形函数”,则实数t的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给图中A,B,C,D,E,F六个区域进行染色,每个区域只染一种颜色,且相邻的区域不同色.若有4种颜色可供选择,则共有___种不同的染色方案.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,若
,若![]() 为抛物线上第一象限的一动点,过
为抛物线上第一象限的一动点,过![]() 作
作![]() 的垂线交准线
的垂线交准线![]() 于点
于点![]() ,交抛物线于
,交抛物线于![]() 两点.
两点.
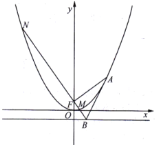
(Ⅰ)求证:直线![]() 与抛物线相切;
与抛物线相切;
(Ⅱ)若点![]() 满足
满足![]() ,求此时点
,求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD-A1B1C1D1中,AB=BC,E,F分别是AB1,BC1的中点.有下列结论:
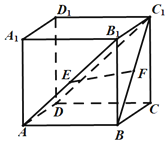
①EF⊥BB1;
②EF∥平面A1B1C1D1;
③EF与C1D所成角为45°;
④EF⊥平面BCC1B1.
其中不成立的是( )
A.②③
B.①④
C.③④
D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】党的十九大报告指出,要以创新理念提升农业发展新动力,引领经济发展走向更高形态.为进一步推进农村经济结构调整,某村举办水果观光采摘节,并推出配套乡村游项目现统计了4月份100名游客购买水果的情况,得到如图所示的频率分布直方图:
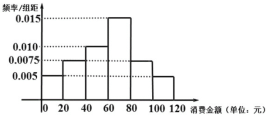
(Ⅰ)若将购买金额不低于![]() 元的游客称为“水果达人”,现用分层抽样的方法从样本的“水果达人”中抽取
元的游客称为“水果达人”,现用分层抽样的方法从样本的“水果达人”中抽取![]() 人,求这
人,求这![]() 人中消费金额不低于
人中消费金额不低于![]() 元的人数;
元的人数;
(Ⅱ)从(Ⅰ)中的![]() 人中抽取
人中抽取![]() 人作为幸运客户免费参加山村旅游项目,请列出所有的基本事件,并求
人作为幸运客户免费参加山村旅游项目,请列出所有的基本事件,并求![]() 人中至少有
人中至少有![]() 人购买金额不低于
人购买金额不低于![]() 元的概率;
元的概率;
(Ⅲ)为吸引顾客,该村特推出两种促销方案,
方案一:每满![]() 元可立减
元可立减![]() 元;
元;
方案二:金额超过![]() 元但又不超过
元但又不超过![]() 元的部分打
元的部分打![]() 折,金额超过
折,金额超过![]() 元但又不超过
元但又不超过![]() 元的部分打
元的部分打![]() 折,金额超过
折,金额超过![]() 元的部分打
元的部分打![]() 折.
折.
若水果的价格为![]() 元/千克,某游客要购买
元/千克,某游客要购买![]() 千克,应该选择哪种方案.
千克,应该选择哪种方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com