【题目】如图，我海监船在
岛海域例行维权巡航，某时刻航行至
处，此时测得其东北方向与它相距32海里的
处有一外国船只，且
岛位于海监船正东
海里处．
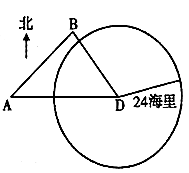
（1）求此时该外国船只与岛的距离；
（2）观测中发现，此外国船只正以每小时8海里的速度沿正南方向航行，为了将该船拦截在离岛24海里处，不让其进入岛24海里内的海域，试确定海监船的航向，并求其速度的最小值．（参考数据：
）
【答案】（1）
；（2）
.
【解析】
试题分析：（1）直接利用余弦定理，求得距离为
；（2）过点
作
于点
，连结
，利用勾股定理和正弦的概念，求得
，故海监船的航向为北偏东
，同时，外国船只到达点
的时间
（小时），海监船的速度
.
试题解析：
（1）依题意，在
中，
，
由余弦定理得
，
∴
．．．．．．．．．．．．．．．．．．．．．．．．．．．．4分
即此时该外国船只与
岛的距离为海里．．．．．．．．．．．．．．．．．．．．．5分
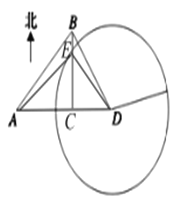
（2）过点作于点，
在
中，
，∴
，．．．．．．．．．．6分
以
为圆心，24为半径的圆交
于点
，连结，
在
中，
，∴
．．．．．．．．．．．．．．．．．7分
又
，
∴
．．．．．．．．．．．．．．．．．9分
外国船只到达点的时间（小时）
∴海监船的速度（海里/小时）．．．．．．．．．．．．．．．．．．11分
故海监船的航向为北偏东，速度的最小值为40海里/小时．．．．．．．．．．12分
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】设等差数列
是无穷数列，且各项均为互不相同的正整数，其前
项和为
，数列
满足
.
（1）若
，求
的值；
（2）若数列
为等差数列，求
；
（3）在（1）的条件下，求证：数列
中存在无穷多项（按原来的顺序）成等比数列.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若对于定义在
上的连续函数
，存在常数
（
），使得
对任意的实数
成立，则称
是回旋函数，且阶数为
.
（1）试判断函数
是否是一个阶数为1的回旋函数，并说明理由；
（2）已知
是回旋函数，求实数
的值；
（3）若回旋函数
（
）在
恰有100个零点，求实数
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
．
（1）若
，判断函数
的单调性；
（2）若函数
在定义域内单调递减，求实数
的取值范围；
（3）当
时，关于
的方程
在
上恰有两个不相等的实数根，求实数
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四棱锥
的底面为直角梯形，
，平面
底面
，
为
的中点，
为正三角形，
是棱
上的一点(异于端点).
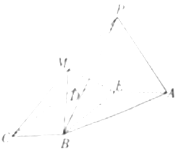
（Ⅰ）若为中点，求证：
平面
；
（Ⅱ）是否存在点，使二面角
的大小为30°.若存在，求出点的位置；若不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费
（单位：千元）对年利润
（单位：万元）的影响，对近5年的宣传费
和年利润
（
）进行了统计，列出了下表：
| 2 | 4 | 7 | 17 | 30 |
| 1 | 2 | 3 | 4 | 5 |
员工小王和小李分别提供了不同的方案．
（1）小王准备用线性回归模型拟合
与
的关系，请你帮助建立
关于
的线性回归方程；（系数精确到0.01）
（2）小李决定选择对数回归模型拟合
与
的关系，得到了回归方程：
，并提供了相关指数
．请用相关指数说明选择哪个模型更合适，并预测年宣传费为4万元的年利润．（精确到0.01）（小王也提供了他的分析分析数据
）
参考公式：相关指数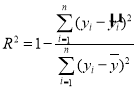
回归方程
中斜率和截距的最小二乘估计公式分别为：
，
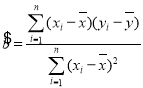．参考数据：
，
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
