
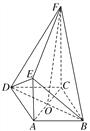
【题目】如图,菱形ABCD中,∠ABC=60°,AC与BD相交于点O,AE⊥平面ABCD,CF∥AE,AB=AE=2.
(1)求证:BD⊥平面ACFE;
(2)当直线FO与平面BED所成的角为45°时,求异面直线OF与BE所成的角的余弦值大小.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)由AE⊥平面ABCD得出AE⊥BD,由菱形性质得BD⊥AC,故BD⊥平面ACFE;
(2)以O为原点建立坐标系,设CF=a,求出![]() 和平面BDE的法向量,利用直线FO与平面BED所成角的大小为45°,可得
和平面BDE的法向量,利用直线FO与平面BED所成角的大小为45°,可得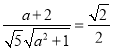 ,即可求出a的值.
,即可求出a的值.
试题解析:
(1)证明:∵四边形ABCD是菱形,
∴BD⊥AC.
∵AE⊥平面ABCD,BD平面ABCD,
∴BD⊥AE.
∵AC∩AE=A,∴BD⊥平面ACFE.
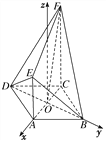
(2)以O为坐标原点,![]() ,
,![]() 的方向为x轴,y轴正方向,过O且平行于CF的直线为z轴(向上为正方向),建立如图所示的空间直角坐标系Oxyz,设CF=a,则B(0,
的方向为x轴,y轴正方向,过O且平行于CF的直线为z轴(向上为正方向),建立如图所示的空间直角坐标系Oxyz,设CF=a,则B(0,![]() ,0),D(0,-
,0),D(0,-![]() ,0),E(1,0,2),F(-1,0,a)(a>0),
,0),E(1,0,2),F(-1,0,a)(a>0),![]() =(-1,0,a).
=(-1,0,a).
设平面BED的法向量为n=(x,y,z),
则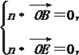 即
即![]()
令z=1,则n=(-2,0,1),
由题意得sin 45°=|cos〈![]() ,n〉|=
,n〉|=![]() =
=![]() =
=![]() ,
,
解得a=3或a=-![]() .
.
由a>0,得a=3,
![]() =(-1,0,3),
=(-1,0,3),![]() =(1,-
=(1,-![]() ,2),
,2),
∴cos〈![]() ,
,![]() 〉=
〉=![]() =
=![]() ,
,
故异面直线OF与BE所成的角的余弦值为![]() .
.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
【题目】某名校从![]() 年到
年到![]() 年考入清华,北大的人数可以通过以下表格反映出来。(为了方便计算,将
年考入清华,北大的人数可以通过以下表格反映出来。(为了方便计算,将![]() 年编号为
年编号为![]() ,
,![]() 年编为
年编为![]() ,以此类推……)
,以此类推……)
年份 |
|
|
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
|
(1)将这![]() 年的数据分为人数不少于
年的数据分为人数不少于![]() 人和少于
人和少于![]() 人两组,按分层抽样抽取
人两组,按分层抽样抽取![]() 年,问考入清华、北大的人数不少于20的应抽多少年?在抽取的这
年,问考入清华、北大的人数不少于20的应抽多少年?在抽取的这![]() 年里,若随机的抽取两年恰有一年考入清华、北大的人数不少于
年里,若随机的抽取两年恰有一年考入清华、北大的人数不少于![]() 的概率是多少?;
的概率是多少?;
(2)根据最近![]() 年的数据,利用最小二乘法求出与之间的线性回归方程,并用以预测
年的数据,利用最小二乘法求出与之间的线性回归方程,并用以预测![]() 年该校考入清华、北大的人数。(结果要求四舍五入至个位)
年该校考入清华、北大的人数。(结果要求四舍五入至个位)
参考公式: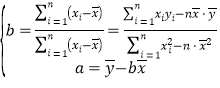
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在标有“甲”的袋中有![]() 个红球和
个红球和![]() 个白球,这些球除颜色外完全相同.
个白球,这些球除颜色外完全相同.
(Ⅰ)若从袋中依次取出![]() 个球,求在第一次取到红球的条件下,后两次均取到白球的概率;
个球,求在第一次取到红球的条件下,后两次均取到白球的概率;
(Ⅱ)现从甲袋中取出个![]() 红球,
红球, ![]() 个白球,装入标有“乙”的空袋.若从甲袋中任取
个白球,装入标有“乙”的空袋.若从甲袋中任取![]() 球,乙袋中任取
球,乙袋中任取![]() 球,记取出的红球的个数为
球,记取出的红球的个数为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
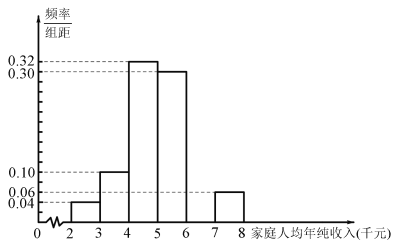
【题目】某贫困地区截至2018年底,按照农村家庭人均年纯收入8000元的小康标准,该地区仅剩部分家庭尚未实现小康.现从这些尚未实现小康的家庭中随机抽取50户,得到这50户家庭2018年的家庭人均年纯收入的频率分布直方图.
(1)补全频率分布直方图,并求出这50户家庭人均年纯收入的中位数和平均数(精确到元);
(2)2019年7月,为估计该地能否在2020年全面实现小康,统计了该地当时最贫困的一个家庭2019年1至6月的人均月纯收入如表:
月份/2019(时间代码 | 1 | 2 | 3 | 4 | 5 | 6 |
人居月纯收入 (元) | 275 | 365 | 415 | 450 | 470 | 485 |
由散点图及相关性分析发现:家庭人均月纯收入![]() 与时间代码
与时间代码![]() 之间具有较强的线性相关关系,请求出回归直线方程;并由此估计该家庭2020年1月的家庭人均月纯收入.
之间具有较强的线性相关关系,请求出回归直线方程;并由此估计该家庭2020年1月的家庭人均月纯收入.
①可能用到的数据:![]() ;
;
②参考公式:线性回归方程![]() 中,
中,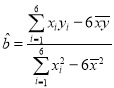 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,GH是东西方向的公路北侧的边缘线,某公司准备在GH上的一点B的正北方向的A处建设一仓库,设![]() ,并在公路北侧建造边长为
,并在公路北侧建造边长为![]() 的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且
的正方形无顶中转站CDEF(其中EF在GH上),现从仓库A向GH和中转站分别修两条道路AB,AC,已知AB=AC+1,且![]() .
.
(1)求![]() 关于
关于![]() 的函数解析式,并求出定义域;
的函数解析式,并求出定义域;
(2)如果中转站四堵围墙造价为10万元/km,两条道路造价为30万元/km,问:![]() 取何值时,该公司建设中转站围墙和两条道路总造价M最低.
取何值时,该公司建设中转站围墙和两条道路总造价M最低.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电力公司在工程招标中是根据技术、商务、报价三项评分标准进行综合评分的,按照综合得分的高低进行综合排序,综合排序高者中标。分值权重表如下:
总分 | 技术 | 商务 | 报价 |
100% | 50% | 10% | 40% |
技术标、商务标基本都是由公司的技术、资质、资信等实力来决定的。报价表则相对灵活,报价标的评分方法是:基准价的基准分是68分,若报价每高于基准价1%,则在基准分的基础上扣0.8分,最低得分48分;若报价每低于基准价1%,则在基准分的基础上加0.8分,最高得分为80分。若报价低于基准价15%以上(不含15%)每再低1%,在80分在基础上扣0.8分。在某次招标中,若基准价为1000(万元)。甲、乙两公司综合得分如下表:
公司 | 技术 | 商务 | 报价 |
甲 | 80分 | 90分 |
|
乙 | 70分 | 100分 |
|
甲公司报价为1100(万元),乙公司的报价为800(万元)则甲,乙公司的综合得分,分别是
A. 73,75.4 B. 73,80 C. 74.6,76 D. 74.6 ,75.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,三点
,三点 中恰有二点在椭圆
中恰有二点在椭圆![]() 上,且离心率为
上,且离心率为![]() 。
。

(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上任一点,
上任一点, ![]() 为椭圆
为椭圆![]() 的左右顶点,
的左右顶点, ![]() 为
为![]() 中点,求证:直线
中点,求证:直线![]() 与直线
与直线![]() 它们的斜率之积为定值;
它们的斜率之积为定值;
(3)若椭圆![]() 的右焦点为
的右焦点为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,求证:直线
,求证:直线![]() 与直线
与直线![]() 斜率之和为定值。
斜率之和为定值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用0,1,2,3,4这五个数字组成无重复数字的自然数.
(Ⅰ)在组成的三位数中,求所有偶数的个数;
(Ⅱ)在组成的三位数中,如果十位上的数字比百位上的数字和个位上的数字都小,则称这个数为“凹数”,如301,423等都是“凹数”,试求“凹数”的个数;
(Ⅲ)在组成的五位数中,求恰有一个偶数数字夹在两个奇数数字之间的自然数的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com