
【题目】设函数f(x)=3sinx+2cosx+1.若实数a,b,c使得af(x)+bf(x﹣c)=1对任意实数x恒成立,则 ![]() 的值为( )
的值为( )
A.﹣1
B.![]()
C.1
D.![]()
【答案】A
【解析】解:由题设可得f(x)= ![]() sin(x+θ)+1,f(x﹣c)=
sin(x+θ)+1,f(x﹣c)= ![]() sin(x+θ﹣c)+1,其中cosθ=
sin(x+θ﹣c)+1,其中cosθ= ![]() ,sinθ=
,sinθ= ![]() (0<θ<
(0<θ< ![]() ),
),
∴af(x)+bf(x﹣c)=1可化成 ![]() asin(x+θ)+
asin(x+θ)+ ![]() bsin(x+θ﹣c)+a+b=1,
bsin(x+θ﹣c)+a+b=1,
即 ![]() (a+bcosc)sin(x+θ)﹣
(a+bcosc)sin(x+θ)﹣ ![]() bsinccos(x+θ)+(a+b﹣1)=0,
bsinccos(x+θ)+(a+b﹣1)=0,
由已知条件,上式对任意x∈R恒成立,故必有 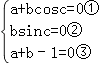 ,
,
若b=0,则式(1)与式(3)矛盾;
故此b≠0,由(2)式得到:sinc=0,
当cosc=1时,有矛盾,故cosc=﹣1,
由①③知a=b= ![]() ,
,
则 ![]() =﹣1.
=﹣1.
故选A
【考点精析】解答此题的关键在于理解两角和与差的正弦公式的相关知识,掌握两角和与差的正弦公式:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn满足2Sn=3an﹣1,其中n∈N* .
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设anbn= ![]() ,求数列{bn}的前n项和为Tn .
,求数列{bn}的前n项和为Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,且
为正方形,且![]() ,其中
,其中![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() ,
,![]() 的中点,动点
的中点,动点![]() 在线段
在线段![]() 上运动时,下列四个结论:①
上运动时,下列四个结论:①![]() ;②
;②![]() ;③
;③![]() 面
面![]() ;④
;④![]() 面
面![]() ,
,
其中恒成立的为( )

A. ①③ B. ③④ C. ①④ D. ②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 的最大值为3,其图象相邻两条对称轴之间的距离为
的最大值为3,其图象相邻两条对称轴之间的距离为![]() .
.
(Ⅰ)求函数![]() 的解析式和当
的解析式和当![]() 时
时![]() 的单调减区间;
的单调减区间;
(Ⅱ)![]() 的图象向右平行移动
的图象向右平行移动![]() 个长度单位,再向下平移1个长度单位,得到
个长度单位,再向下平移1个长度单位,得到![]() 的图象,用“五点法”作出
的图象,用“五点法”作出![]() 在
在![]() 内的大致图象.
内的大致图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 是等比数列,下列命题正确的个数为( )
是等比数列,下列命题正确的个数为( )
① ![]() 、
、![]() 均为等比数列; ②
均为等比数列; ②![]() 成等差数列;
成等差数列;
③![]() 、
、![]() 成等比数列; ④
成等比数列; ④![]() 、
、![]() 均为等比数列
均为等比数列
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,F是椭圆C: ![]() (a>b>0)的左焦点,A,B分别为C的左,右顶点.P为C上一点,且PF⊥x轴,过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为( )
(a>b>0)的左焦点,A,B分别为C的左,右顶点.P为C上一点,且PF⊥x轴,过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(13分)设{an}是公比为正数的等比数列a1=2,a3=a2+4.
(Ⅰ)求{an}的通项公式;
(Ⅱ)设{bn}是首项为1,公差为2的等差数列,求数列{an+bn}的前n项和Sn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com