[题目]如图为四棱锥P﹣ABCD的表面展开图.四边形ABCD为矩形. .AD=1．已知顶点P在底面ABCD上的射影为点A.四棱锥的高为 .则在四棱锥P﹣ABCD中.PC与平面ABCD所成角的正切值为．题目和参考答案——青夏教育精英家教网—

【题目】如图为四棱锥P﹣ABCD的表面展开图，四边形ABCD为矩形，，AD=1．已知顶点P在底面ABCD上的射影为点A，四棱锥的高为，则在四棱锥P﹣ABCD中，PC与平面ABCD所成角的正切值为．

【答案】
【解析】解：作出四棱锥的直观图如图所示：
∵顶点P在底面ABCD上的射影为点A，∴PA⊥平面ABCD，
∴∠PCA为直线PC与平面ABCD所成的角，PA= ．
∵四边形ABCD为矩形，，AD=1，
∴AC= ，
∴tan∠PCA= ．
所以答案是：．

【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点，需要掌握已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则才能正确解答此题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

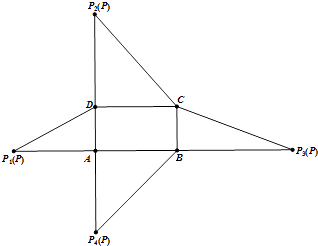
科目：高中数学 来源： 题型：

【题目】在奥运会射箭决赛中，参赛号码为1～4号的4名射箭运动员参加射箭比赛．
（1）通过抽签将他们安排到1～4号靶位，试求恰有2名运动员所抽靶位号与其参赛号码相同的概率；
（2）记1号、2号射箭运动员射箭的环数为ξ（ξ所有取值为0，1，2，3，…，10）分别为P1 ， P2 ．根据教练员提供的资料，其概率分布如下表：

ξ	1	2	3	4	5	6	7	8	9	10
P1	0	0	0	0.06	0.04	0.06	0.3	0.2	0.3	0.04
P2	0	0	0	0.04	0.05	0.05	0.2	0.32	0.32	0.02

①若1，2号运动员各射箭一次，求两人中至少有一人命中9环的概率；
②判断1号、2号射箭运动员谁射箭的水平高？并说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】直线l过直线x+y﹣2=0和直线x﹣y+4=0的交点，且与直线3x﹣2y+4=0平行，求直线l的方程．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=a（x+a）（x﹣a+3），g（x）=2x+2﹣1，若对任意x∈R，f（x）＞0和g（x）＞0至少有一个成立，则实数a的取值范围是（）
A.（1，2）
B.（2，3）
C.（﹣2，﹣1）∪（1，+∞）
D.（0，2）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数的定义域为集合A，函数g（x）=lg（x2﹣2x+a）的定义域为集合B．（Ⅰ）当a=﹣8时，求A∩B；
（Ⅱ）若A∩RB={x|﹣1＜x≤3}，求a的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，四棱锥P﹣ABCD的底面ABCD为直角梯形，AD‖BC，且，BC⊥DC，∠BAD=60°，平面PAD⊥底面ABCD，E为AD的中点，△PAD为等边三角形，M是棱PC上的一点，设（M与C不重合）．

（1）求证：CD⊥DP；
（2）若PA∥平面BME，求k的值；
（3）若二面角M﹣BE﹣A的平面角为150°，求k的值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】若[x]表示不超过x的最大整数，则[lg2]+[lg3]+…+lg[2017]+[lg ]+[lg ]+…+[lg ]= ．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=﹣x2+2|x﹣a|，x∈R．
（1）若函数f（x）为偶函数，求实数a的值；
（2）当x=﹣1时，函数f（x）在x=﹣1取得最大值，求实数a的取值范围．
（3）若函数f（x）有三个零点，求实数a的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知A，B，C为锐角△ABC的内角， =（sinA，sinBsinC）， =（1，﹣2）， ⊥ ．
（1）tanB，tanBtanC，tanC能否构成等差数列？并证明你的结论；
（2）求tanAtanBtanC的最小值．

查看答案和解析>>

同步练习册答案