
 (a>0,b>0)
(a>0,b>0)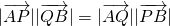 ,求证点Q总在某定直线上.
,求证点Q总在某定直线上. (a>0,b>0),过双曲线外一点P(m,n)的动直线l与双曲线C相交与不同两点A,B时,在线段AB上取点Q,满足
(a>0,b>0),过双曲线外一点P(m,n)的动直线l与双曲线C相交与不同两点A,B时,在线段AB上取点Q,满足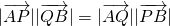 ,则点Q在哪条定直线上?
,则点Q在哪条定直线上?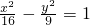 .
. 均不为零,记
均不为零,记  ,则λ>0且λ≠1
,则λ>0且λ≠1
 ,
, ,
, ,
,
 ①,
①, ②,
②,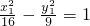 ③,
③, ④,
④, (a>0,b>0),过双曲线外一点P(m,n)的动直线l与双曲线C相交与不同两点A,B时,在线段AB上取点Q,满足
(a>0,b>0),过双曲线外一点P(m,n)的动直线l与双曲线C相交与不同两点A,B时,在线段AB上取点Q,满足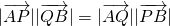 ,
, (a>0,b>0),过椭圆外一点P(m,n)的动直线l与椭圆C相交与不同两点A,B时,在线段AB上取点Q,满足
(a>0,b>0),过椭圆外一点P(m,n)的动直线l与椭圆C相交与不同两点A,B时,在线段AB上取点Q,满足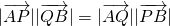 ,得出点Q在定直线b2mx+a2ny=a2b2上;
,得出点Q在定直线b2mx+a2ny=a2b2上; ,
,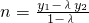 ,
, ,
,
 ①,
①, ②,
②, ③,
③, ④,
④,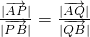 ,设其比值为λ则有
,设其比值为λ则有  、
、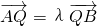 ,此时利用定比分点定理可得A、B、P三点横坐标关系及纵坐标关系,同时可得A、B、Q三点横坐标关系及纵坐标关系,又因为点A、B的坐标满足双曲线方程,再利用已得关系式可整体替换,同时消去参数λ,最后得到变量x、y的关系式,则问题得证.
,此时利用定比分点定理可得A、B、P三点横坐标关系及纵坐标关系,同时可得A、B、Q三点横坐标关系及纵坐标关系,又因为点A、B的坐标满足双曲线方程,再利用已得关系式可整体替换,同时消去参数λ,最后得到变量x、y的关系式,则问题得证. (a>0,b>0),过双曲线外一点P(m,n)的动直线l与双曲线C相交与不同两点A,B时,在线段AB上取点Q,满足
(a>0,b>0),过双曲线外一点P(m,n)的动直线l与双曲线C相交与不同两点A,B时,在线段AB上取点Q,满足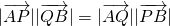 ,得出点Q在那条定直线上;
,得出点Q在那条定直线上; (a>0,b>0),过椭圆外一点P(m,n)的动直线l与椭圆C相交与不同两点A,B时,在线段AB上取点Q,满足
(a>0,b>0),过椭圆外一点P(m,n)的动直线l与椭圆C相交与不同两点A,B时,在线段AB上取点Q,满足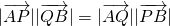 ,得出点Q在定直线b2mx+a2ny=a2b2上.
,得出点Q在定直线b2mx+a2ny=a2b2上.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
(08年潍坊市六模)(12分)已知双曲线C:![]() (a>0,b>0),B是右顶点,F是右焦点,点A在x轴正半轴上,且满足
(a>0,b>0),B是右顶点,F是右焦点,点A在x轴正半轴上,且满足![]() 、
、![]() 、
、![]() 成等比数列,过F作双曲线C在第一、第三象限的渐近线的垂线l,垂足为P.
成等比数列,过F作双曲线C在第一、第三象限的渐近线的垂线l,垂足为P.
(1)求证:![]() ;
;
(2)若l与双曲线C的左、右两支分别相交于点D、E,求双曲线C的离心率e的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求证:![]() ·
·![]() =
=![]() ·
·![]() ;
;
(2)若l与双曲线C的左、右两支分别交于点D、E,求双曲线C的离心率e的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)求证:![]() ·
·![]() =
=![]() ·
·![]() ;
;
(2)若l与双曲线C的左、右两支分别相交于点D、E,求双曲线离心率e的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013年全国普通高等学校招生统一考试理科数学(全国大纲卷解析版) 题型:解答题
已知双曲线C: (a>0,b>0)的左、右焦点分别为
(a>0,b>0)的左、右焦点分别为 、
、 ,离心率为3,直线y=2与C的两个交点间的距离为
,离心率为3,直线y=2与C的两个交点间的距离为 .
.
(Ⅰ)求a,b;
(Ⅱ)设过 的直线l与C的左、右两支分别交于A、B两点,且
的直线l与C的左、右两支分别交于A、B两点,且 ,证明:
,证明: 、
、 、
、 成等比数列.
成等比数列.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省扬州中学高三(上)周练数学试卷(12.22)(解析版) 题型:填空题
 (a>0)的一条渐近线与直线l:2x-y+1=0垂直,则实数a= .
(a>0)的一条渐近线与直线l:2x-y+1=0垂直,则实数a= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com