练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系xOy中，曲线C的参数方程为 （α为参数），在以原点为极点，X轴正半轴为极轴的极坐标系中，直线l的极坐标方程为ρsin（θ﹣ ）= ．
    （1）求C的普通方程和l的倾斜角；
    （2）若l和C交于A，B两点，且Q（2，3），求|QA|+|QB|．

    【答案】
    （1）解：曲线C的参数方程为 （α为参数），普通方程是 =1

    由ρsin（θ﹣ ）= ，得ρsinθ﹣ρcosθ=1

    所以：x﹣y+1=0，即直线l的倾斜角为：45°


    （2）解：联立直线与椭圆的方程，解得A（0，1），B（﹣ ，﹣ ）

    所以|QA|=2 ，|QB|=

    所以|QA|+|QB|=


    【解析】（1）消去参数求C的普通方程；求出l的直角坐标方程，即可求出l的倾斜角；（2）若l和C交于A，B两点，求出A，B的坐标，利用Q（2，3），求|OA|+|QB|．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，已知椭圆C的中心为原点O，F（﹣2 ，0）为C的左焦点，P为C上一点，满足|OP|=|OF|且|PF|=4，则椭圆C的方程为（ ）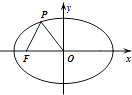
    A. =1
    B. =1
    C. =1
    D. =1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥P﹣ABC中，AB=AC=PB=PC=10，PA=8，BC=12，点M在平面PBC内，且AM=7，设异面直线AM与BC所成角为α，则cosα的最大值为（ ）

    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的两个焦点为 ， 是椭圆上一点，若 ， ．
    （1）求椭圆的方程；
    （2）直线l过右焦点 （不与x轴重合）且与椭圆相交于不同的两点A，B，在x轴上是否存在一个定点P（x0 ， 0），使得 的值为定值？若存在，写出P点的坐标（不必求出定值）；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2cos（ ﹣x）cos（x+ ）+ ． （Ⅰ）求函数f（x）的最小正周期和单调递减区间；
    （Ⅱ）求函数f（x）在区间[0， ]上的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某区选派7名队员代表本区参加全市青少年围棋锦标赛，其中3名来自A学校且1名为女棋手，另外4名来自B学校且2名为女棋手．从这7名队员中随机选派4名队员参加第一阶段的比赛．
    （1）求在参加第一阶段比赛的队员中，恰有1名女棋手的概率；
    （2）设X为选出的4名队员中A、B两校人数之差的绝对值，求随机变量X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x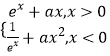）= ，若函数f（x）有四个零点，则实数a的取值范围是（ ）
    A.（﹣∞，﹣e）
    B.（﹣∞，﹣ ）
    C.（﹣∞，﹣ ）
    D.（﹣∞，﹣ ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C的离心率为 ，F1 ， F2分别为椭圆的左右焦点，P为椭圆上任意一点，△PF1F2的周长为 ，直线l：y=kx+m（k≠0）与椭圆C相交于A，B两点． （Ⅰ）求椭圆C的标准方程；
    （Ⅱ）若直线l与圆x2+y2=1相切，过椭圆C的右焦点F2作垂直于x轴的直线，与椭圆相交于M，N两点，与线段AB相交于一点（与A，B不重合）．求四边形MANB面积的最大值及取得最大值时直线l的方程；
    （Ⅲ）若|AB|=2，试判断直线l与圆x2+y2=1的位置关系．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】[选修4-4：坐标系与参数方程]

    在直角坐标系xoy中，曲线C1的参数方程为 （β为参数）．以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=4cosθ．
    （Ⅰ）将曲线C1的方程化为极坐标方程；
    （Ⅱ）已知直线l的参数方程为 （ ＜α＜π，t为参数，t≠0），l与C1交与点A，l与C2交与点B，且|AB|= ，求α的值．

    查看答案和解析>>

    同步练习册答案