
分析 画出正方体,可以看出所有与AB平行的棱和平面A1B1CD成0°角,容易说明BC1⊥平面A1B1CD,从而可以求出其它棱和该平面成的角都为45°.可以看出面对角线B1C,A1D和平面A1B1CD成0°角,而由前面知BC1,AD1和该平面成90°角,其它的面对角线和该平面所成角按线面角的求法求出即可.
解答  解:如图,
解:如图,
AB∥平面A1B1CD;
∴和AB平行的棱与平面A1B1CD所成角为0°;
设BC1与B1C交于点O,∵A1B1⊥平面BCC1B1,BC1?平面BCC1B1;
∴BC1⊥A1B1,又BC1⊥B1C,A1B1∩B1C=B1;
∴BC1⊥平面A1B1CD;
∴∠BB1O是BB1和平面A1B1CD所成角,且为45°;
∴和BB1平行的棱与平面A1B1CD所成角为45°;
同样可得到BC和平面A1B1CD所成角为45°;
∴各棱与平面A1B1CD所成角可为:0°,45°;
面对角线A1D和B1C都在平面A1B1CD内,∴这两条对角线和该平面所成角为0°;
BC1⊥平面A1B1CD,∴BC1,AD1和该平面成90°角;
连接A1O,则∠C1A1O为面对角线A1C1所成角;
在Rt△OA1C1中,A1C1=2C1O;
∴$sin∠{C}_{1}{A}_{1}O=\frac{1}{2}$;
∴∠C1A1O=30°;
同理可以求出其它对角线和该平面成的角都为30°;
∴各面对角线和平面A1B1CD所成角可为:0°,90°,30°.
故答案为:0°,45°;0°,90°,30°.
点评 考查正方形的对角线互相垂直,线面垂直的性质,及线面垂直的判定定理,以及直线和平面所成角的定义及求法.


科目:高中数学 来源: 题型:选择题
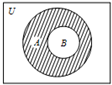 设全集U=R,集合A、B满足如图所示的关系,且A={x|x2-2x-3≤0},阴影部分表示的集合为{x|-1≤x<1},则集合B可以是( )
设全集U=R,集合A、B满足如图所示的关系,且A={x|x2-2x-3≤0},阴影部分表示的集合为{x|-1≤x<1},则集合B可以是( )| A. | {x|1<x<3} | B. | {x|1<x≤3} | C. | {x|1≤x<3} | D. | {x|1≤x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
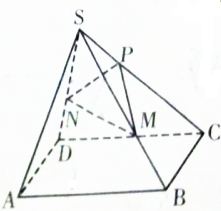 如图,四边形ABCD是正方形,S为四边形ABCD所在平面外一点,SA=SB=SC=SD,P,M,N分别是SC,SB,SD上的点,且PC:SP=SM:MB=SN:ND=2:1,求证:SA∥平面PMN.
如图,四边形ABCD是正方形,S为四边形ABCD所在平面外一点,SA=SB=SC=SD,P,M,N分别是SC,SB,SD上的点,且PC:SP=SM:MB=SN:ND=2:1,求证:SA∥平面PMN.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
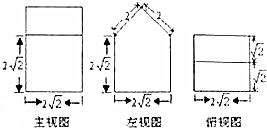
| A. | 16$\sqrt{2}$cm3 | B. | 32$\sqrt{2}$cm3 | C. | 24$\sqrt{2}$cm3 | D. | 20$\sqrt{2}$cm3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com