
【题目】现有6名奥运会志愿者,其中志愿者![]() 通晓日语,
通晓日语, ![]() 通晓俄语,
通晓俄语, ![]() 通晓韩语,从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语,从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
(1)求![]() 被选中的概率;
被选中的概率;
(2)求![]() 和
和![]() 不全被选中的概率;
不全被选中的概率;
(3)若6名奥运会志愿者每小时派两人值班,现有两名只会日语的运动员到来,求恰好遇到![]() 的概率.
的概率.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:
(1)可用列举法列出从6人中选出日语、俄语和韩语志愿者各1名的一切可能的结果组成的基本事件,共8个,其中有![]() 的有4个,由概率公式计算可得;
的有4个,由概率公式计算可得;
(2)可从对立事件考虑, ![]() 全被选中有两种可能,由此可得概率;
全被选中有两种可能,由此可得概率;
(3)6人中任选2人有15种选法,而恰好遇到![]() 只有一种可能,故可得概率.
只有一种可能,故可得概率.
试题解析:
(1)从6人中选出日语、俄语和韩语志愿者各1名,其一切可能的结果组成的基本事件是: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . 由8个基本事件组成,由于每一个基本事件被抽取的机会均等,因此,这些基本事件的发生是等可能的.
. 由8个基本事件组成,由于每一个基本事件被抽取的机会均等,因此,这些基本事件的发生是等可能的.
用![]() 表示“
表示“![]() 恰被选中”这一事件,则
恰被选中”这一事件,则![]() 为
为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,事件
,事件![]() 由4个基本事件组成,因而
由4个基本事件组成,因而![]() .
.
(2)用![]() 表示“
表示“![]() 不全被选中”这一事件,则其对立事件
不全被选中”这一事件,则其对立事件![]() 表示“
表示“![]() 全被选中”这一事件,由于
全被选中”这一事件,由于![]() ,事件
,事件![]() 有2个基本事件组成,
有2个基本事件组成,
所以![]() ,由对立事件的概率公式得
,由对立事件的概率公式得![]() .
.
(3)∵6名奥运会志愿者每小时派两人值班,共有![]() 种情况,
种情况,
而恰好遇到![]() 的情况只有1种,
的情况只有1种,
故恰好遇到![]() 的概率为
的概率为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】命题p:关于x的不等式x2+2ax+4>0对于一切x∈R恒成立,命题q:x∈11,2], x2-a≥0,若p∨q为真,p∧q为假,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,以
,以![]() 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,和平面内一点
,和平面内一点![]() (
(![]() ),过点
),过点![]() 任作直线
任作直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,设直线
两点,设直线![]() ,
, ![]() ,
, ![]() 的斜率分别为
的斜率分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,试求
,试求![]() ,
, ![]() 满足的关系式.
满足的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三次函数![]() ,下列命题正确的是 .
,下列命题正确的是 .
①函数![]() 关于原点
关于原点![]() 中心对称;
中心对称;
②以![]() ,
,![]() 两不同的点为切点作两条互相平行的切线,分别与
两不同的点为切点作两条互相平行的切线,分别与![]() 交于
交于![]() 两点,则这四个点的横坐标满足关系
两点,则这四个点的横坐标满足关系![]() ;
;
③以![]() 为切点,作切线与
为切点,作切线与![]() 图像交于点
图像交于点![]() ,再以点
,再以点![]() 为切点作直线与
为切点作直线与![]() 图像交于点
图像交于点![]() ,再以点
,再以点![]() 作切点作直线与
作切点作直线与![]() 图像交于点
图像交于点![]() ,则
,则![]() 点横坐标为
点横坐标为![]() ;
;
④若![]() ,函数
,函数![]() 图像上存在四点
图像上存在四点![]() ,使得以它们为顶点的四边形有且仅有一个正方形.
,使得以它们为顶点的四边形有且仅有一个正方形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有两枚大小相同、质地均匀的正四面体玩具,每个玩具的各个面上上分别写着数字1,2,3,5,同时投掷这两枚玩具一次,记![]() 为两个朝下的面上的数字之和.
为两个朝下的面上的数字之和.
(1)求事件“![]() 不小于6”的概率;
不小于6”的概率;
(2)“![]() 为奇数”的概率和“
为奇数”的概率和“![]() 为偶数”的概率是不是相等?证明你作出的结论.
为偶数”的概率是不是相等?证明你作出的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,椭圆
,椭圆![]() 过点
过点 ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,且
,且![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 的上顶点,过点
的上顶点,过点![]() 分别作直线
分别作直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为![]() ,且
,且![]() ,证明:直线
,证明:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1是四棱锥的直观图,其正(主)视图和侧(左)视图均为直角三角形,俯视图外框为矩形,相关数据如图2所示.
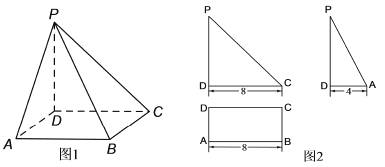
(1)设![]() 中点为
中点为![]() ,在直线
,在直线![]() 上找一点
上找一点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(2)若二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() ,求四棱锥
,求四棱锥![]() 的外接球的表面积.
的外接球的表面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com