
【题目】已知函数f(x)=x2﹣x,g(x)=ex﹣ax﹣1(e为自然对数的底数).
(1)讨论函数g(x)的单调性;
(2)当x>0时,f(x)≤g(x)恒成立,求实数a的取值范围.
【答案】
(1)解:∵g(x)=ex﹣ax﹣1,∴g'(x)=ex﹣a
①若a≤0,g'(x)>0,g(x)在(﹣∞,+∞)上单调递增;
②若a>0,当x∈(﹣∞,lna]时,g'(x)<0,g(x)单调递减;
当x∈(lna,+∞)时,g'(x)>0,g(x)单调递增.
(2)解:当x>0时,x2﹣x≤ex﹣ax﹣1,即 ![]()
令 ![]() ,则
,则 ![]()
令φ(x)=ex(x﹣1)﹣x2+1(x>0),则φ'(x)=x(ex﹣2)
当x∈(0,ln2)时,φ'(x)<0,φ(x)单调递减;
当x∈(ln2,+∞)时,φ'(x)>0,φ(x)单调递增
又φ(0)=0,φ(1)=0,
∴当x∈(0,1)时,φ(x)<0,即h'(x)<0,∴h(x)单调递减;
当x∈(0,+∞)时,φ(x)=(x﹣1)(ex﹣x﹣1>0,即h'(x)>0,
∴h(x)单调递增,
∴h(x)min=h(1)=e﹣1,
∴实数a的取值范围是(﹣∞,e﹣1].
【解析】(1)求出g'(x)=ex﹣a,由a≤0和a>0分类讨论,由此能求出结果.(2)当x>0时, ![]() 令
令 ![]() ,则
,则 ![]() 令φ(x)=ex(x﹣1)﹣x2+1(x>0),则φ'(x)=x(ex﹣2),由此利用导数性质能求出实数a的取值范围.
令φ(x)=ex(x﹣1)﹣x2+1(x>0),则φ'(x)=x(ex﹣2),由此利用导数性质能求出实数a的取值范围.
【考点精析】关于本题考查的利用导数研究函数的单调性和函数的最大(小)值与导数,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.
比较,其中最大的是一个最大值,最小的是最小值才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】在某班举行的“庆五一”联欢晚会开幕前已排好有8个不同节目的节目单,如果保持原来的节目相对顺序不变,临时再插进去![]() 三个不同的新节目,且插进的三个新节目按
三个不同的新节目,且插进的三个新节目按![]() 顺序出场,那么共有__________种不同的插入方法(用数字作答).
顺序出场,那么共有__________种不同的插入方法(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|x2-3x+2=0},B={x|x2+(a-1)x+a2-5=0}.
(1)若A∩B={2},求实数a的值;
(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分) 某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取![]() 份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在
份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在![]() ,
,![]() 的学生人数为6.
的学生人数为6.
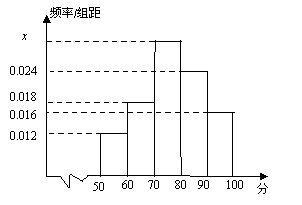
(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)试估计所抽取的数学成绩的平均数;
(Ⅲ)试根据样本估计“该校高一学生期末数学考试成绩![]() ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某科研课题组通过一款手机APP软件,调查了某市1000名跑步爱好者平均每周的跑步量(简称“周跑量”),得到如下的频数分布表
周跑量(km/周) |
|
|
|
|
|
|
|
|
|
人数 | 100 | 120 | 130 | 180 | 220 | 150 | 60 | 30 | 10 |
(1)在答题卡上补全该市1000名跑步爱好者周跑量的频率分布直方图:
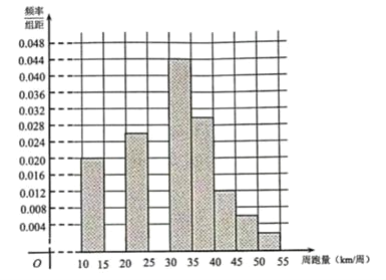
注:请先用铅笔画,确定后再用黑色水笔描黑
(2)根据以上图表数据计算得样本的平均数为![]() ,试求样本的中位数(保留一位小数),并用平均数、中位数等数字特征估计该市跑步爱好者周跑量的分布特点
,试求样本的中位数(保留一位小数),并用平均数、中位数等数字特征估计该市跑步爱好者周跑量的分布特点
(3)根据跑步爱好者的周跑量,将跑步爱好者分成以下三类,不同类别的跑者购买的装备的价格不一样,如下表:
周跑量 | 小于20公里 | 20公里到40公里 | 不小于40公里 |
类别 | 休闲跑者 | 核心跑者 | 精英跑者 |
装备价格(单位:元) | 2500 | 4000 | 4500 |
根据以上数据,估计该市每位跑步爱好者购买装备,平均需要花费多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、F分别是椭圆C: ![]() +
+ ![]() =1(a>b>0)的左顶点、右焦点,点P为椭圆C上一动点,当PF⊥x轴时,AF=2PF.
=1(a>b>0)的左顶点、右焦点,点P为椭圆C上一动点,当PF⊥x轴时,AF=2PF.
(1)求椭圆C的离心率;
(2)若椭圆C存在点Q,使得四边形AOPQ是平行四边形(点P在第一象限),求直线AP与OQ的斜率之积;
(3)记圆O:x2+y2= ![]() 为椭圆C的“关联圆”.若b=
为椭圆C的“关联圆”.若b= ![]() ,过点P作椭圆C的“关联圆”的两条切线,切点为M、N,直线MN的横、纵截距分别为m、n,求证:
,过点P作椭圆C的“关联圆”的两条切线,切点为M、N,直线MN的横、纵截距分别为m、n,求证: ![]() +
+ ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为线段
分别为线段![]() 上的点,且
上的点,且![]() ,
, ![]() ,
, ![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成的锐二面角.
所成的锐二面角.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com