
【题目】已知![]() ,
,![]() 是动点,以
是动点,以![]() 为直径的圆与圆
为直径的圆与圆![]() :
:![]() 内切.
内切.
(1)求![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设![]() 是圆
是圆![]() 与
与![]() 轴的交点,过点
轴的交点,过点![]() 的直线与
的直线与![]() 交于
交于![]() 两点,直线
两点,直线![]() 交直线
交直线![]() 于点
于点![]() ,求证:
,求证:![]() 三点共线.
三点共线.
科目:高中数学 来源: 题型:
【题目】如图,![]() 正方形
正方形![]() 所在平面,M是
所在平面,M是![]() 的中点,二面角
的中点,二面角![]() 的大小为
的大小为![]() .
.

(1)设l是平面![]() 与平面
与平面![]() 的交线,证明
的交线,证明![]() ;
;
(2)在棱![]() 是否存在一点N,使
是否存在一点N,使![]() 为
为![]() 的二面角.若不存在,说明理由:若存在,求
的二面角.若不存在,说明理由:若存在,求![]() 长.
长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知p:函数f(x)在R上是增函数,f(m2)<f(m+2)成立;q:方程![]() 1(m∈R)表示双曲线.
1(m∈R)表示双曲线.
(1)若p为真命题,求m的取值范围;
(2)若p∨q为真,p∧q为假,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
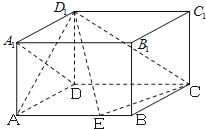
【题目】已知在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(Ⅰ)求证:D1E⊥A1D;
(Ⅱ)在棱AB上是否存在点E使得AD1与平面D1EC成的角为![]() ?若存在,求出AE的长,若不存在,说明理由.
?若存在,求出AE的长,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() 在圆内,在过点P所作的圆的所有弦中,弦长最小值为
在圆内,在过点P所作的圆的所有弦中,弦长最小值为![]() .
.
(1)求实数a的值;
(2)若点M为圆外的动点,过点M向圆C所作的两条切线始终互相垂直,求点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于无穷数列![]() ,若正整数
,若正整数![]() ,使得当
,使得当![]() 时,有
时,有![]() ,则称
,则称![]() 为“
为“![]() 不减数列”.
不减数列”.
(1)设![]() ,
,![]() 均为正整数,且
均为正整数,且![]() ,甲:
,甲:![]() 为“
为“![]() 不减数列”,乙:
不减数列”,乙:![]() 为“
为“![]() 不减数列”.试判断命题:“甲是乙的充分条件”的真假,并说明理由;
不减数列”.试判断命题:“甲是乙的充分条件”的真假,并说明理由;
(2)已知函数![]() 与函数
与函数![]() 的图象关于直线
的图象关于直线![]() 对称,数列
对称,数列![]() 满足
满足![]() ,
,![]() ,如果
,如果![]() 为“
为“![]() 不减数列”,试求
不减数列”,试求![]() 的最小值;
的最小值;
(3)对于(2)中的![]() ,设
,设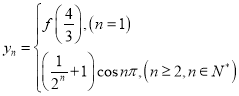 ,且
,且![]() .是否存在实数
.是否存在实数![]() 使得
使得![]() 为“
为“![]() 不减数列”?若存在,求出
不减数列”?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是古希腊数学家阿基米德用平衡法求球的体积所用的图形.此图由正方形![]() 、半径为
、半径为![]() 的圆及等腰直角三角形构成,其中圆内切于正方形,等腰三角形的直角顶点与
的圆及等腰直角三角形构成,其中圆内切于正方形,等腰三角形的直角顶点与![]() 的中点
的中点![]() 重合,斜边在直线
重合,斜边在直线![]() 上.已知
上.已知![]() 为
为![]() 的中点,现将该图形绕直线
的中点,现将该图形绕直线![]() 旋转一周,则阴影部分旋转后形成的几何体积为( )
旋转一周,则阴影部分旋转后形成的几何体积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】血药浓度(Serum Drug Concentration)是指药物吸收后在血浆内的总浓度(单位:mg/ml),通常用血药浓度来研究药物的作用强度.下图为服用同等剂量的三种新药后血药浓度的变化情况,其中点![]() 的横坐标表示服用第
的横坐标表示服用第![]() 种药后血药浓度达到峰值时所用的时间,其它点的横坐标分别表示服用三种新药后血药浓度第二次达到峰值一半时所用的时间(单位:h),点
种药后血药浓度达到峰值时所用的时间,其它点的横坐标分别表示服用三种新药后血药浓度第二次达到峰值一半时所用的时间(单位:h),点![]() 的纵坐标表示第
的纵坐标表示第![]() 种药的血药浓度的峰值.(
种药的血药浓度的峰值.(![]() )
)

①记![]() 为服用第
为服用第![]() 种药后达到血药浓度峰值时,血药浓度提高的平均速度,则
种药后达到血药浓度峰值时,血药浓度提高的平均速度,则![]() 中最大的是_______;
中最大的是_______;
②记![]() 为服用第
为服用第![]() 种药后血药浓度从峰值降到峰值的一半所用的时间,则
种药后血药浓度从峰值降到峰值的一半所用的时间,则![]() 中最大的是_______
中最大的是_______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“爱国,是人世间最深层、最持久的情感,是一个人立德之源、立功之本。”在中华民族几千年绵延发展的历史长河中,爱国主义始终是激昂的主旋律。爱国汽车公司拟对“东方红”款高端汽车发动机进行科技改造,根据市场调研与模拟,得到科技改造投入![]() (亿元)与科技改造直接收益
(亿元)与科技改造直接收益![]() (亿元)的数据统计如下:
(亿元)的数据统计如下:
| 2 | 3 | 4 | 6 | 8 | 10 | 13 | 21 | 22 | 23 | 24 | 25 |
| 13 | 22 | 31 | 42 | 50 | 56 | 58 | 68.5 | 68 | 67.5 | 66 | 66 |
当![]() 时,建立了
时,建立了![]() 与
与![]() 的两个回归模型:模型①:
的两个回归模型:模型①:![]() ;模型②:
;模型②:![]() ;当
;当![]() 时,确定
时,确定![]() 与
与![]() 满足的线性回归方程为:
满足的线性回归方程为:![]() .
.
(1)根据下列表格中的数据,比较当![]() 时模型①、②的相关指数
时模型①、②的相关指数![]() ,并选择拟合精度更高、更可靠的模型,预测对“东方红”款汽车发动机科技改造的投入为17亿元时的直接收益.
,并选择拟合精度更高、更可靠的模型,预测对“东方红”款汽车发动机科技改造的投入为17亿元时的直接收益.
回归模型 | 模型① | 模型② |
回归方程 |
|
|
| 182.4 | 79.2 |
(附:刻画回归效果的相关指数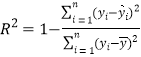 ,
,![]() .)
.)
(2)为鼓励科技创新,当科技改造的投入不少于20亿元时,国家给予公司补贴收益10亿元,以回归方程为预测依据,比较科技改造投入17亿元与20亿元时公司实际收益的大小;
(附:用最小二乘法求线性回归方程![]() 的系数公式
的系数公式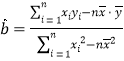
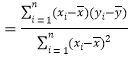 ;
;![]() )
)
(3)科技改造后,“东方红”款汽车发动机的热效![]() 大幅提高,
大幅提高,![]() 服从正态分布
服从正态分布![]() ,公司对科技改造团队的奖励方案如下:若发动机的热效率不超过
,公司对科技改造团队的奖励方案如下:若发动机的热效率不超过![]() ,不予奖励;若发动机的热效率超过
,不予奖励;若发动机的热效率超过![]() 但不超过
但不超过![]() ,每台发动机奖励2万元;若发动机的热效率超过
,每台发动机奖励2万元;若发动机的热效率超过![]() ,每台发动机奖励5万元.求每台发动机获得奖励的数学期望.
,每台发动机奖励5万元.求每台发动机获得奖励的数学期望.
(附:随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() .)
.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com