
分析 (1)将θ=0和θ=$\frac{π}{2}$分别代入直线l的极坐标方程,求出ρ,从而得出两点的极坐标,画出直线;
(2)分别求出直线l和曲线ρ=1的直角坐标方程,要求圆上任意一点到直线l的最短距离,只要求圆心O(0,0)到直线l的距离即可.
解答 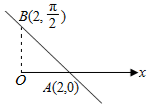 解:(1)直线l经过A(2,0),$B(2,\frac{π}{2})$两点,
解:(1)直线l经过A(2,0),$B(2,\frac{π}{2})$两点,
在极坐标系下,直线如图所示:
(2)曲线ρ=1化为直角坐标方程得x2+y2=1,该曲线为单位圆,
将直线l的极坐标方程$ρsin(θ+\frac{π}{4})=\sqrt{2}$化为直角坐标方程得x+y-2=0
要求圆上任意一点到直线l的最短距离,只要求圆心O(0,0)到直线l的距离即可.
由点到直线的距离公式得:$d=\frac{|0+0-2|}{{\sqrt{2}}}=\sqrt{2}$,
所以点Q到直线l的最短距离为$\sqrt{2}-1$,
此时,点Q的极坐标为$Q(1,\frac{π}{4})$.
点评 本题考查了极坐标方程化为直角坐标方程,考查了圆上一点到直线的最短距离的求法,属于中档题.


科目:高中数学 来源: 题型:解答题
| 几何题 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=x-\frac{1}{x}$ | B. | y=lg|x| | C. | $y=\root{3}{x}$ | D. | $y=\sqrt{x^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com