
【题目】已知等比数列{an}满足:|a2﹣a3|=10,a1a2a3=125.
(1)求数列{an}的通项公式;
(2)是否存在正整数m,使得 ![]() ?若存在,求m的最小值;若不存在,说明理由.
?若存在,求m的最小值;若不存在,说明理由.
【答案】
(1)解:设等比数列{an}的公比为q,则由已知可得 ![]()
解得 
故 ![]() .
.
(2)解:若 ![]() ,则
,则 ![]() ,
,
故 ![]() 是首项为
是首项为 ![]() ,公比为
,公比为 ![]() 的等比数列,
的等比数列,
从而  .
.
若 ![]() ,则
,则 ![]() 是首项为
是首项为 ![]() ,公比为﹣1的等比数列,
,公比为﹣1的等比数列,
从而  故
故 ![]() .
.
综上,对任何正整数m,总有 ![]() .
.
故不存在正整数m,使得 ![]() 成立.
成立.
【解析】(1)设等比数列{an}的公比为q,结合等比数列的通项公式表示已知条件,解方程可求a1 , q,进而可求通项公式(2)结合(I)可知 ![]() 是等比数列,结合等比数列的求和公式可求
是等比数列,结合等比数列的求和公式可求 ![]() ,即可判断
,即可判断
【考点精析】关于本题考查的等比数列的通项公式(及其变式)和数列的前n项和,需要了解通项公式:![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系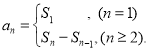 才能得出正确答案.
才能得出正确答案.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组调查学生使用智能手机对学习成绩的影响,部分统计数据如下表:
使用智能手机 | 不使用智能手机 | 总计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
总计 | 20 | 10 | 30 |
(Ⅰ)根据以上![]() 列联表判断,能否在犯错误的概率不超过0.005的前提下认为使用智能手机对学习成绩有影响?
列联表判断,能否在犯错误的概率不超过0.005的前提下认为使用智能手机对学习成绩有影响?
(Ⅱ)从学习成绩优秀的12名同学中,随机抽取2名同学,求抽到不使用智能手机的人数![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.05 | 0,。025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直棱柱ABCD﹣A1B1C1D1中,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=AA1=3. 
(1)证明:AC⊥B1D;
(2)求直线B1C1与平面ACD1所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小区抽取100户居民进行月用电量调查,发现其用电量都在50至350度之间,频率分布直方图如图所示: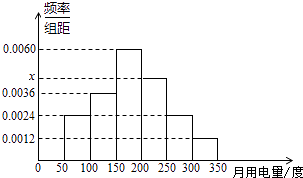
(Ⅰ)直方图中x的值为;
(Ⅱ)在这些用户中,用电量落在区间[100,250)内的户数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网站从春节期间参与收发网络红包的手机用户中随机抽取10000名进行调查,将受访用户按年龄分成5组:![]() 并整理得到如下频率分布直方图:
并整理得到如下频率分布直方图:
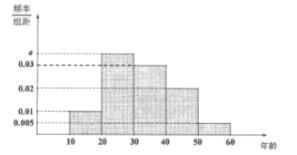
(1)求![]() 的值;
的值;
(2)从春节期间参与收发网络红包的手机用户中随机抽取一人,估计其年龄低于40岁的概率;
(3)估计春节期间参与收发网络红包的手机用户的平均年龄。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点. 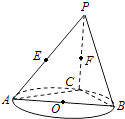
(1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明;
(2)设(1)中的直线l与圆O的另一个交点为D,且点Q满足 ![]() .记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
.记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设n是正整数,r为正有理数.
(1)求函数f(x)=(1+x)r+1﹣(r+1)x﹣1(x>﹣1)的最小值;
(参考数据: ![]() .
.
(2)证明: ![]() ;
;
(3)设x∈R,记[x]为不小于x的最小整数,例如 ![]() .令
.令 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com