
分析 将一颗骰子(它的六个面分别标有点数1,2,3,4,5,6)先后抛掷两次,共有36种不同情况;
(1)两数之积是6的倍数的情况有15种,
(2)满足logx2y=1,即x=2y的情况有3种,
(3)满足点(x,y)在直线x-y=3的下方区域,即x-y>3的情况有3种,
代入概率公式,可得答案.
解答 解:将一颗骰子(它的六个面分别标有点数1,2,3,4,5,6)先后抛掷两次,共有36种不同情况;
(1)两数之积是6的倍数的情况有:
(1,6),(2,3),(2,6),(3,2),(3,4),
(3,6),(4,3),(4,6),(5,6),(6,1),
(6,2),(6,3),(6,4),(6,5),(6,6),共15个,
故两数之积是6的倍数的概率P=$\frac{15}{36}$=$\frac{5}{12}$;
(2)若logx2y=1,则x=2y,
满足条件的情况有:(2,1),(4,2),(6,3)共3种;
故logx2y=1的概率P=$\frac{3}{36}$=$\frac{1}{12}$;
(3)满足点(x,y)在直线x-y=3的下方区域,即x-y>3的情况有:
(5,1),(6,1),(6,2)共3种;
故点(x,y)在直线x-y=3的下方区域的概率P=$\frac{3}{36}$=$\frac{1}{12}$;
点评 本题考查的知识点古典概型概率计算公式,难度不大,属于基础题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:选择题
| A. | $y=x+1与y=\frac{{{x^2}+x}}{x}$ | B. | $f(x)=\frac{x^2}{{{{({\sqrt{x}})}^2}}}与g(x)=x$ | ||
| C. | $f(x)=x\frac{|x|}{x}与f(t)=\left\{\begin{array}{l}t(t>0)\\-t(t<0)\end{array}\right.$ | D. | $f(x)=|x|与g(x)=\left\{\begin{array}{l}x(x>0)\\-x(x<0)\end{array}\right.$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
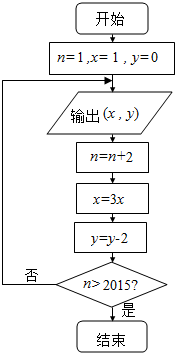 某算法的流程图如图所示,记输出的数组(x,y)依次为(x1,y1),(x2,y2),…(x3,y3)…,若程序运行中输出的一个数组是(9,y),则y=-4;程序结束时,共输出(x,y)的组数为1008.
某算法的流程图如图所示,记输出的数组(x,y)依次为(x1,y1),(x2,y2),…(x3,y3)…,若程序运行中输出的一个数组是(9,y),则y=-4;程序结束时,共输出(x,y)的组数为1008.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com