
【题目】设数列{an}满足a1=1,且an+1-an=n+1(n∈N*),则数列{an}的通项公式为________; ![]() 前10项的和为________.
前10项的和为________.
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的两条渐近线与抛物线
的两条渐近线与抛物线![]() 的准线分别交于A,B两点,O为坐标原点,若
的准线分别交于A,B两点,O为坐标原点,若![]() ,则双曲线的离心率
,则双曲线的离心率![]() __________.
__________.
【答案】![]()
【解析】因为双曲线![]() 的两条渐近线为
的两条渐近线为![]() ,抛物线
,抛物线![]() 的准线为
的准线为![]() ,所以
,所以![]() ,
,
因此![]()
点睛:解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于![]() 的方程或不等式,再根据
的方程或不等式,再根据![]() 的关系消掉
的关系消掉![]() 得到
得到![]() 的关系式,而建立关于
的关系式,而建立关于![]() 的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.
的方程或不等式,要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.
【题型】填空题
【结束】
16
【题目】若函数![]() 满足:对于
满足:对于![]() 图象上任意一点P,在其图象上总存在点
图象上任意一点P,在其图象上总存在点![]() ,使得
,使得![]() 成立,称函数
成立,称函数![]() 是“特殊对点函数”.给出下列五个函数:
是“特殊对点函数”.给出下列五个函数:
①![]() ;②
;②![]() (其中e为自然对数的底数);③
(其中e为自然对数的底数);③![]() ;④
;④![]() ;
;
⑤![]() .
.
其中是“特殊对点函数”的序号是__________.(写出所有正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 分别是椭圆C:
分别是椭圆C: ![]() 的左、右焦点,其中右焦点为抛物线
的左、右焦点,其中右焦点为抛物线![]() 的焦点,点
的焦点,点 在椭圆C上.
在椭圆C上.
(1)求椭圆C的标准方程;
(2)设与坐标轴不垂直的直线![]() 过
过![]() 与椭圆C交于A、B两点,过点
与椭圆C交于A、B两点,过点 且平行直线
且平行直线![]() 的直线交椭圆C于另一点N,若四边形MNBA为平行四边形,试问直线
的直线交椭圆C于另一点N,若四边形MNBA为平行四边形,试问直线![]() 是否存在?若存在,请求出
是否存在?若存在,请求出![]() 的斜率;若不存在,请说明理由.
的斜率;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂用7万元钱购买了一台新机器,运输安装费用2千元,每年投保、动力消耗的费用也为2千元,每年的保养、维修、更换易损零件的费用逐年增加,第一年为2千元,第二年为3千元,第三年为4千元,依此类推,即每年增加1千元.
(1)求使用n年后,保养、维修、更换易损零件的累计费用S(千元)关于n的表达式;
(2)问这台机器最佳使用年限是多少年?并求出年平均费用(单位:千元)的最小值.(最佳使用年限是指使年平均费用最小的时间,年平均费用=(购入机器费用+运输安装费用+每年投保、动力消耗的费用+保养、维修、更换易损零件的累计费用)÷机器使用的年数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法中错误的是( )
A. 设![]() ,则“
,则“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
B. 若![]() 为真命题,则
为真命题,则![]() ,
, ![]() 中至少有一个为真命题
中至少有一个为真命题
C. 命题:“若![]() 是幂函数,则
是幂函数,则![]() 的图象不经过第四象限”的否命题是假命题
的图象不经过第四象限”的否命题是假命题
D. 命题“![]() ,
, ![]() 且
且![]() ”的否定形式是“
”的否定形式是“![]() ,
, ![]() 且
且![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】3月12日,全国政协总工会界别小组会议上,人社部副部长汤涛在回应委员呼声时表示无论是从养老金方面,还是从人力资源的合理配置来说,延迟退休是大势所趋.不过,汤部长也表示,不少职工对于延迟退休有着不同的意见.某高校一社团就是否同意延迟退休的情况随机采访了200名市民,并进行了统计,得到如下的![]() 列联表:
列联表:
赞同延迟退休 | 不赞同延迟退休 | 合计 | |
男性 | 80 | 20 | 100 |
女性 | 60 | 40 | 100 |
合计 | 140 | 60 | 200 |
(1)根据上面的列联表判断能否有![]() 的把握认为对延迟退休的态度与性别有关;
的把握认为对延迟退休的态度与性别有关;
(2)为了进一步征求对延迟退休的意见和建议,从抽取的200位市民中对不赞同的按照分层抽样的方法抽取6人,再从这6人中随机抽出3名进行电话回访,求3人中至少有1人为男性的概率.
附: 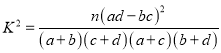 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某移动支付公司随机抽取了100名移动支付用户进行调查,得到如下数据:
每周移动支付次数 | 1次 | 2次 | 3次 | 4次 | 5次 | 6次及以上 |
男 | 4 | 3 | 3 | 7 | 8 | 30 |
女 | 6 | 5 | 4 | 4 | 6 | 20 |
合计 | 10 | 8 | 7 | 11 | 14 | 50 |
(1)在每周使用移动支付超过3次的样本中,按性别用分层抽样随机抽取5名用户.
①求抽取的5名用户中男、女用户各多少人;
②从这5名用户中随机抽取2名用户,求抽取的2名用户均为男用户的概率.
(2)如果认为每周使用移动支付次数超过3次的用户“喜欢使用移动支付”,能否在犯错误概率不超过0.05的前提下,认为“喜欢使用移动支付”与性别有关?
附表及公式: 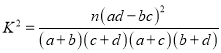
| 0.50 | 0.25 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 0.455 | 1.323 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com