
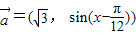 ,
,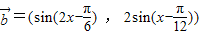 ,
,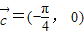 .定义函数f(x)=
.定义函数f(x)=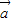 •
•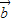 .
.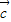 方向移动后,再将其各点横坐标变为原来的2倍得到y=g(x)的图象,求y=g(x)的单调递减区间及g(x)取得最大值时所有x的集合.
方向移动后,再将其各点横坐标变为原来的2倍得到y=g(x)的图象,求y=g(x)的单调递减区间及g(x)取得最大值时所有x的集合.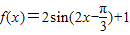
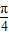 个单位,再将其各点横坐标变为原来的2倍得到y=g(x)的图象,故
个单位,再将其各点横坐标变为原来的2倍得到y=g(x)的图象,故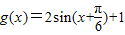 ,再由正弦类函数的性质求单调减区间与函数取到最大值自变量的集合即可.
,再由正弦类函数的性质求单调减区间与函数取到最大值自变量的集合即可.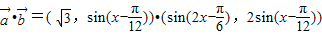
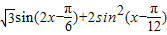
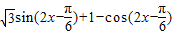
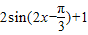
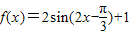
 方向移动,即向左平移
方向移动,即向左平移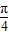 个单位,
个单位,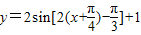 ,即
,即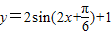 ,
,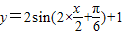 ,
,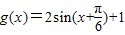 .
.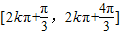 ,k∈Z
,k∈Z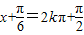 ,即
,即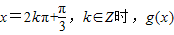 的最大值为3,
的最大值为3,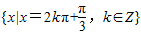 .
.

科目:高中数学 来源:2009-2010学年山东省聊城市水城中学高三(上)期末数学试卷(文科)(解析版) 题型:解答题
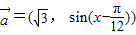 ,
,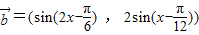 ,
,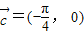 .定义函数f(x)=
.定义函数f(x)= •
•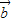 .
.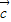 方向移动后,再将其各点横坐标变为原来的2倍得到y=g(x)的图象,求y=g(x)的单调递减区间及g(x)取得最大值时所有x的集合.
方向移动后,再将其各点横坐标变为原来的2倍得到y=g(x)的图象,求y=g(x)的单调递减区间及g(x)取得最大值时所有x的集合.查看答案和解析>>
科目:高中数学 来源:2010年安徽省合肥市高校附中高三联考数学试卷(理科)(解析版) 题型:选择题
 ,
, ,下面关于函数f(x)的导函数f'(x)说法中错误的是( )
,下面关于函数f(x)的导函数f'(x)说法中错误的是( ) 为减函数
为减函数 对称
对称 个单位长度得到
个单位长度得到查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求f(x)的解析式;
(2)求f(x)的单调递增区间;
(3)如果△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,试求x的范围及此时函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源:2008-2009学年重庆市南开中学高一(下)期末复习数学试卷(解析版) 题型:解答题
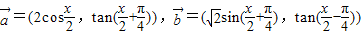 ,令
,令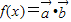 .求函数f(x)的最大值,最小正周期,并写出
.求函数f(x)的最大值,最小正周期,并写出查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com