
【题目】某市一农产品近六年的产量统计如下表:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量 | 5.1 | 5.3 | 5.6 | 5.5 | 6.0 | 6.1 |
观察表中数据看出,可用线性回归模型拟合![]() 与
与![]() 的关系.
的关系.
(1)根据表中数据,将以下表格空白部分的数据填写完整,并建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
|
|
|
|
|
| 总和 | 均值 | |
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| 5.1 | 5.3 | 5.6 | 5.5 | 6.0 | 6.1 | ||
| 1 | 4 | 9 | 16 | 25 | 36 | ||
| 5.1 | 10.6 | 16.8 | 22 | 30 | 36.6 | 121.1 |
(2)若在2025年之前该农产品每千克的价格![]() (单位:元)与年产量
(单位:元)与年产量![]() 满足的关系式为
满足的关系式为![]() ,且每年该农产品都能全部销售.预测在2013~2025年之间,某市该农产品的销售额
,且每年该农产品都能全部销售.预测在2013~2025年之间,某市该农产品的销售额![]() 在哪一年达到最大.
在哪一年达到最大.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: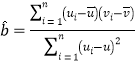
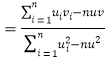 ,
,![]() .
.
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
【题目】下列四个命题:①任意两条直线都可以确定一个平面;②若两个平面有3个不同的公共点,则这两个平面重合;③直线a,b,c,若a与b共面,b与c共面,则a与c共面;④若直线l上有一点在平面α外,则l在平面α外.其中错误命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 垂直于
垂直于![]() 轴的直线与抛物线
轴的直线与抛物线![]() 相交于
相交于![]() 两点,抛物线
两点,抛物线![]() 在
在![]() 两点处的切线及直线
两点处的切线及直线![]() 所围成的三角形面积为
所围成的三角形面积为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)设![]() 是抛物线
是抛物线![]() 上异于原点
上异于原点![]() 的两个动点,且满足
的两个动点,且满足![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,直角梯形
,直角梯形![]() 通过直角梯形
通过直角梯形![]() 以直线
以直线![]() 为轴旋转得到,且使得平面
为轴旋转得到,且使得平面![]() 平面
平面![]() .
. ![]() 为线段
为线段![]() 的中点,
的中点, ![]() 为线段
为线段![]() 上的动点.
上的动点.

(![]() )求证:
)求证: ![]() .
.
(![]() )当点
)当点![]() 满足
满足![]() 时,求证:直线
时,求证:直线![]() 平面
平面![]() .
.
(![]() )当点
)当点![]() 是线段
是线段![]() 中点时,求直线
中点时,求直线![]() 和平面
和平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]()
![]() ,动点
,动点![]() 满足
满足![]() ,
,![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过定点![]() 作直线
作直线![]() 交曲线
交曲线![]() 于
于![]()
![]() 两点.设
两点.设![]() 为坐标原点,若直线
为坐标原点,若直线![]() 与
与![]() 轴垂直,求
轴垂直,求![]() 面积的最大值;
面积的最大值;
(3)设![]() ,在
,在![]() 轴上,是否存在一点
轴上,是否存在一点![]() ,使直线
,使直线![]() 和
和![]() 的斜率的乘积为非零常数?若存在,求出点
的斜率的乘积为非零常数?若存在,求出点![]() 的坐标和这个常数;若不存在,说明理由.
的坐标和这个常数;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+x-6y+m=0与直线l:x+2y-3=0.
(1)若直线l与圆C没有公共点,求m的取值范围;
(2)若直线l与圆C相交于P、Q两点,O为原点,且OP⊥OQ,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代儒家提出的“六艺”指:礼乐射御书数.某校国学社团预在周六开展“六艺”课程讲座活动,周六这天准备排课六节,每艺一节,排课有如下要求:“乐”与“书”不能相邻,“射”和“御”要相邻,则针对“六艺”课程讲座活动的不同排课顺序共有( )
A.18种B.36种C.72种D.144种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com