Question

7．把半椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（x≥0）与圆弧（x-c）²+y²=a²（x＜0）合成的曲线称作“曲圆”，其中F（c，0）为半椭圆的右焦点．如图，A₁，A₂，B₁，B₂
分别是“曲圆”与x轴、y轴的交点，已知∠B₁FB₂=$\frac{2π}{3}$，扇形FB₁A₁B₂的面
积为$\frac{4π}{3}$．
（1）求a，c的值； 
（2）过点F且倾斜角为θ的直线交“曲圆”于P，Q两点，试将△A₁PQ的周长L表示为θ的函数；
（3）在（2）的条件下，当△A₁PQ的周长L取得最大值时，试探究△A₁PQ的面积是否为定值？若是，请求出该定值；若不是，请求出面积的取值范围．

Answer 1

分析 （1）由扇形FB₁A₁B₂的面积为可得a，在△OFB₂中，tan∠OFB₂=tan60°=$\frac{b}{c}=\sqrt{3}$，又因为c²+b²=a²，可得c．
（2）分 ①当θ∈（0，$\frac{π}{3}$）；  ②当θ∈（$\frac{2π}{3}，π$）；  ③当θ∈（$\frac{π}{3}$，$\frac{2π}{3}$）求出△A₁PQ的周长；
 （3）在（2）的条件下，当△A₁PQ的周长L取得最大值时P、Q在半椭圆：$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$（x≥0）上，
利用弦长公式、点到直线的距离公式，表示面积，再利用单调性求出范围．

解答 解：（1）∵扇形FB₁A₁B₂的面积为$\frac{1}{2}×\frac{2π}{3}×{a}^{2}$=$\frac{4π}{3}$，∴a=2，圆弧（x-c）²+y²=a²（x＜0）与y轴交点B₂（0，b），
在△OFB₂中，tan∠OFB₂=tan60°=$\frac{b}{c}=\sqrt{3}$，又因为c²+b²=a²，∴c=1．
（2）显然直线PQ的斜率不能为0（θ∈（0，π）），故设PQ方程为：x=my+1
由（1）得半椭圆方程为：$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$（x≥0）与圆弧方程为：（x-1）²+y²=4（x＜0），且A₁（-1，0）恰为椭圆的左焦点．
①当θ∈（0，$\frac{π}{3}$）时，P、Q分别在圆弧：（x-1）²+y²=4（x＜0）、半椭圆：$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$（x≥0）上，
△A₁PO为腰为2的等腰三角形|A₁P|=4sin$\frac{θ}{2}$，
△A₁PQ的周长L=|QA₁|+|QF|+|PF|+|A₁P|=2a+a+|A₁P|=6+4sin$\frac{θ}{2}$，
②当θ∈（$\frac{2π}{3}，π$）时，P、Q分别在圆弧：（x-1）²+y²=4（x＜0）、半椭圆：$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$（x≥0）上，
△A₁PO为腰为2的等腰三角形|A₁P|=4cos$\frac{θ}{2}$，
△A₁PQ的周长L=|QA₁|+|QF|+|PF|+|A₁P|=2a+a+|A₁P|=6+4cos$\frac{θ}{2}$，
③当θ∈（$\frac{π}{3}$，$\frac{2π}{3}$）时，P、Q在半椭圆：$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$（x≥0）上，
△A₁PO为腰为2的等腰三角形|A₁P|=4sin$\frac{θ}{2}$，
△A₁PQ的周长L=|QA₁|+|QF|+|PF|+|A₁P|=4a=8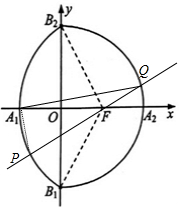

 （3）在（2）的条件下，当△A₁PQ的周长L取得最大值时P、Q在半椭圆：$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$（x≥0）上，
联立$\left\{\begin{array}{l}{x=my+1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$得（3m²+4）y²+6my-9=0
y₁+y₂=$\frac{-6m}{3+4{m}^{2}}$，y₁y_2⁼$\frac{-9}{3{m}^{2}+4}$．
|PQ|=$\sqrt{1+{m}^{2}}\frac{\sqrt{144+144{m}^{2}}}{3{m}^{2}+4}=\frac{12（{m}^{2}+1）}{3{m}^{2}+4}$，点A₁到PQ的距离d=$\frac{2}{\sqrt{1+{m}^{2}}}$．
△A₁PQ的面积s=$\frac{1}{2}$|PQ|•d=12$\frac{\sqrt{{m}^{2}+1}}{3{m}^{2}+4}$．
令m²+1=t，t∈[1，$\frac{4}{3}$]，s=12$\frac{\sqrt{{m}^{2}+1}}{3{m}^{2}+4}$=12$\sqrt{\frac{t}{9{t}^{2}+6t+1}}=\sqrt{\frac{1}{9t+\frac{1}{t}+6}}$；
∵g（t）=9t+$\frac{1}{t}$在[1，+$\frac{4}{3}$]上递增，∴g（1）≤g（t）≤g（$\frac{4}{3}$），；10≤g（t）≤$\frac{75}{4}$，
 $\frac{8\sqrt{3}}{5}$≤s≤3
∴△A₁PQ的面积不为定值，面积的取值范围为：[$\frac{8\sqrt{3}}{5}，3$]

点评 本题考查椭圆中参数的求法，考查三角形周长的最大值满足的条件的证明，考查弦长的取值范围的求法，解题时要认真审题，注意椭圆弦长公式的合理运用