
【题目】已知函数![]() (
(![]() ),曲线
),曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直.
垂直.
(1)试比较![]() 与
与![]() 的大小,并说明理由;
的大小,并说明理由;
(2)若函数![]() 有两个不同的零点
有两个不同的零点![]() ,证明:
,证明: ![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】试题分析:(Ⅰ)求出f(x)的导数,由两直线垂直的条件:斜率相等,即可得到切线的斜率和切点坐标,进而f(x)的解析式和导数,求出单调区间,可得f(2016)>f(2017),即可得到20162017与20172016的大小;
(Ⅱ)运用分析法证明,不妨设x1>x2>0,由根的定义可得所以化简得lnx1﹣kx1=0,lnx2﹣kx2=0.可得lnx1+lnx2=k(x1+x2),lnx1﹣lnx2=k(x1﹣x2),要证明, ![]() ,即证明lnx1+lnx2>2,也就是k(x1+x2)>2.求出k,即证
,即证明lnx1+lnx2>2,也就是k(x1+x2)>2.求出k,即证![]() ,令
,令![]() ,则t>1,即证
,则t>1,即证![]() .令
.令![]() (t>1).求出导数,判断单调性,即可得证.
(t>1).求出导数,判断单调性,即可得证.
试题解析:
(1)依题意得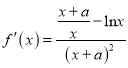 ,
,
所以![]() ,又由切线方程可得
,又由切线方程可得![]() ,即
,即![]() ,解得
,解得![]()
此时![]() ,
, ![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() ;
;
令![]() ,即
,即![]() ,解得
,解得![]()
所以![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]()
所以![]() ,即
,即![]() ,
,
![]() ,
, ![]() .
.
(2)证明:不妨设![]() 因为
因为![]()
所以化简得![]() ,
, ![]()
可得![]() ,
, ![]() .
.
要证明![]() ,即证明
,即证明![]() ,也就是
,也就是![]()
因为![]() ,所以即证
,所以即证![]()
即![]() ,令
,令![]() ,则
,则![]() ,即证
,即证![]() .
.
令![]() (
(![]() ),由
),由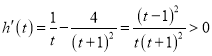
故函数![]() 在
在![]() 是增函数,所以
是增函数,所以![]() ,即
,即![]() 得证.
得证.
所以![]() .
.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】若方程x2+ax+2b=0的一个根在(0,1)内,另一个根在(1,2)内,则 ![]() 的取值范围是( )
的取值范围是( )
A.[﹣2,1)
B.(﹣2,1)
C.(﹣∞,﹣2)∪(1,+∞)
D.(﹣∞,﹣2]∪[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1= ![]() 且an+1=an﹣an2(n∈N*)
且an+1=an﹣an2(n∈N*)
(1)证明:1< ![]() ≤2(n∈N*);
≤2(n∈N*);
(2)设数列{an2}的前n项和为Sn , 证明 ![]() (n∈N*).
(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 |
时间代号t | 1 | 2 | 3 | 4 | 5 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
(1)求y关于t的回归方程 ![]() .
.
(2)用所求回归方程预测该地区2015年(t=6)的人民币储蓄存款.
附:回归方程 ![]() 中
中 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,
, ![]() 的四个顶点构成的四边形面积为
的四个顶点构成的四边形面积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)在椭圆![]() 上是否存在相异两点
上是否存在相异两点![]() ,使其满足:①直线
,使其满足:①直线![]() 与直线
与直线![]() 的斜率互为相反数;②线段
的斜率互为相反数;②线段![]() 的中点在
的中点在![]() 轴上,若存在,求出
轴上,若存在,求出![]() 的平分线与椭圆相交所得弦的弦长;若不存在,请说明理由.
的平分线与椭圆相交所得弦的弦长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com