【题目】设函数
，若
，使得直线
的斜率为0，则
的最小值为（ ）
A. -8 B. 
C. -6 D. 2
【答案】C
【解析】函数f（x）=﹣x2﹣6x+m，
对称轴x=﹣3，开口向下，
当x∈[﹣5，﹣2]的值域M：f（﹣5）≤M≤f（﹣3），即m+5≤M≤9+m．
函数g（x）=2x3+3x2﹣12x﹣m，
则g′（x）=6x2+6x﹣12．
令g′（x）=0，
可得：x=﹣2或1．
当x∈（﹣∞，﹣2）和（1，+∞）时，g′（x）＞0，则g（x）是递增函数．
当x∈（﹣2，1）时，g′（x）＜0，则g（x）是递减函数．
∵x∈[﹣1，2]
∴g（1）min=﹣7﹣m
g（﹣1）=13﹣m，g（2）=4﹣m．
∴g（x）值域N：﹣7﹣m≤N≤13﹣m．
由题意，MN
则
，
解得：2≥m≥﹣6．
∴m的最小值为﹣6．
故选：C．
开心蛙状元测试卷系列答案科目：高中数学 来源： 题型：
【题目】如图，矩形
中， 
， 
为边
的中点，将
沿直线
翻转成
.若
为线段
的中点，则在
翻折过程中：
①
是定值；②点
在某个球面上运动；
③存在某个位置，使
；④存在某个位置，使
平面
.
其中正确的命题是_________.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】动点
到定点
的距离比它到直线
的距离小1，设动点
的轨迹为曲线
，过点
的直线交曲线
于
、
两个不同的点，过点
、
分别作曲线
的切线，且二者相交于点
.
（1）求曲线
的方程；
（2）求证： 
；
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆
过点
，
，且圆心在直线
上，过点
作直线
与圆
：
交于两点
，
.
（1）求圆的方程；
（2）当
时，若于圆交于
，
且
，求直线的方程；
（3）若点恰好是线段
的中点，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某高校在2010年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组：第1组
，第2组
，第3组
，第4组
，第5组
，得到的频率分布直方图如图所示。
（1）求第3、4、5组的频率；
（2）为了能选拔出最优秀的学生，该校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试，求第3、4、5组每组各抽取多少学生进入第二轮面试？
（3）在（2）的前提下，学校决定在这6名学生中随机抽取2名学生接受甲考官的面试，求第4组至少有一名学生被甲考官面试的概率。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若曲线C上任意一点与直线
上任意一点的距离都大于1,则称曲线C远离”直线，在下列曲线中,“远离”直线：y=2x的曲线有___________(写出所有符合条件的曲线的编号)
①曲线C:
；②曲线C:
；③曲线C:
；
④曲线C:
；⑤曲线C:
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在推导很多三角恒等变换公式时，我们可以利用平面向量的有关知识来研究，在一定程度上可以简化推理过程.如我们就可以利用平面向量来推导两角差的余弦公式:
具体过程如下：
如图，在平面直角坐标系
内作单位圆O，以
为始边作角
.它们的终边与单位圆O的交点分别为A，B.
则
由向量数量积的坐标表示，有：
设
的夹角为θ，则
另一方面，由图3.1—3（1）可知，
；由图可知，
.于是
.
所以
，也有，
所以，对于任意角
有：（
）
此公式给出了任意角的正弦、余弦值与其差角
的余弦值之间的关系，称为差角的余弦公式，简记作.
有了公式以后，我们只要知道
的值，就可以求得
的值了.
阅读以上材料，利用下图单位圆及相关数据（图中M是AB的中点），采取类似方法（用其他方法解答正确同等给分）解决下列问题：
（1）判断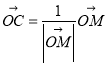
是否正确？（不需要证明）
（2）证明：
（3）利用以上结论求函数
的单调区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
