
科目:高中数学 来源: 题型:
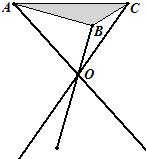 某厂根据市场需求开发折叠式小凳(如图所示)、凳面为三角形的尼龙布,凳脚为三根细钢管、考虑到钢管的受力和人的舒适度等因素,设计小凳应满足:①凳子高度为30cm,②三根细钢管相交处的节点O与凳面三角形ABC重心的连线垂直于凳面和地面.
某厂根据市场需求开发折叠式小凳(如图所示)、凳面为三角形的尼龙布,凳脚为三根细钢管、考虑到钢管的受力和人的舒适度等因素,设计小凳应满足:①凳子高度为30cm,②三根细钢管相交处的节点O与凳面三角形ABC重心的连线垂直于凳面和地面.查看答案和解析>>
科目:高中数学 来源:上海高考真题 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:
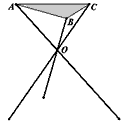
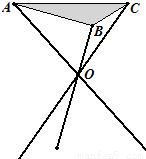
某厂根据市场需求开发折叠式小凳(如图所示). 凳面为三角形的尼龙布,凳脚为三根细钢管. 考虑到钢管的受力和人的舒适度等因素,设计小凳应满足:① 凳子高度为30cm,② 三根细钢管相交处的节点O与凳面三角形ABC重心的连线垂直于凳面和地面.
(1)若凳面是边长为![]() 的正三角形,三只凳脚与地面所成的角均为
的正三角形,三只凳脚与地面所成的角均为![]() ,确定节点
,确定节点![]() 分细钢管上下两段的比值(精确到
分细钢管上下两段的比值(精确到![]() );
);
(2)若凳面是顶角为![]() 的等腰三角形,腰长为
的等腰三角形,腰长为![]() ,节点
,节点![]() 分细钢管上下两段之比为
分细钢管上下两段之比为![]() . 确定三根细钢管的长度(精确到
. 确定三根细钢管的长度(精确到![]()
![]() ).
).

查看答案和解析>>
科目:高中数学 来源:2008年上海市春季高考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com