
【题目】设集合![]() ,
,![]() .
.
(1)若![]() ,求实数
,求实数![]() 的值;
的值;
(2)若![]() ,求实数
,求实数![]() 的范围.
的范围.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)∵![]() ∴AB,又B中最多有两个元素,∴A=B,从而得到实数
∴AB,又B中最多有两个元素,∴A=B,从而得到实数![]() 的值;(2)求出集合A、B的元素,利用B是A的子集,即可求出实数a的范围.
的值;(2)求出集合A、B的元素,利用B是A的子集,即可求出实数a的范围.
(1)∵![]() ∴AB,又B中最多有两个元素,
∴AB,又B中最多有两个元素,
∴A=B,
∴x=0,﹣4是方程x2+2(a+1)x+a2﹣1=0的两个根,
故a=1;
(2)∵A={x|x2+4x=0,x∈R}
∴A={0,﹣4},
∵B={x|x2+2(a+1)x+a2﹣1=0},且BA.
故①B=时,△=4(a+1)2﹣4(a2﹣1)<0,即a<﹣1,满足BA;
②B≠时,当a=﹣1,此时B={0},满足BA;
当a>﹣1时,x=0,﹣4是方程x2+2(a+1)x+a2﹣1=0的两个根,
故a=1;
综上所述a=1或a≤﹣1;


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点在原点
的顶点在原点![]() ,对称轴是
,对称轴是![]() 轴,且过点
轴,且过点![]() .
.
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)已知斜率为![]() 的直线
的直线![]() 交
交![]() 轴于点
轴于点![]() ,且与曲线
,且与曲线![]() 相切于点
相切于点![]() ,点
,点![]() 在曲线
在曲线![]() 上,且直线
上,且直线![]() 轴,
轴, ![]() 关于点
关于点![]() 的对称点为
的对称点为![]() ,判断点
,判断点![]() 是否共线,并说明理由.
是否共线,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在约束条件 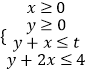 下,当t≥0时,其所表示的平面区域的面积为S(t),S(t)与t之间的函数关系用下列图象表示,正确的应该是( )
下,当t≥0时,其所表示的平面区域的面积为S(t),S(t)与t之间的函数关系用下列图象表示,正确的应该是( )
A.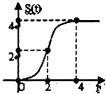
B.
C.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司引进一条价值30万元的产品生产线,经过预测和计算,得到生产成本降低![]() 万元与技术改造投入
万元与技术改造投入![]() 万元之间满足:①
万元之间满足:①![]() 与
与![]() 和
和![]() 的乘积成正比;②当
的乘积成正比;②当![]() 时,
时, ![]() ,并且技术改造投入比率
,并且技术改造投入比率![]() ,
, ![]() 为常数且
为常数且![]() .
.
(1)求![]() 的解析式及其定义域;
的解析式及其定义域;
(2)求![]() 的最大值及相应的
的最大值及相应的![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() ,满足
,满足![]() ,
,![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若关于![]() 的不等式
的不等式![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 的两个零点分别在区间
的两个零点分别在区间![]() 和
和![]() 内,求实数
内,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于实数x,符号[x]表示不超过x的最大整数,例如[π]=3,[﹣1.08]=﹣2,定义函数f(x)=x﹣[x],则下列命题中正确的是
①函数f(x)的最大值为1; ②函数f(x)的最小值为0;
③方程![]() 有无数个根; ④函数f(x)是增函数.
有无数个根; ④函数f(x)是增函数.
A. ②③ B. ①②③ C. ② D. ③④
查看答案和解析>>
科目:高中数学 来源: 题型:
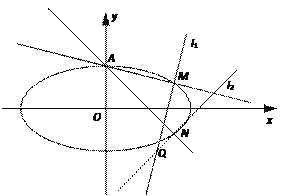
【题目】在平面直角坐标系xOy中,已知椭圆C: ![]() (a>b>0)的一条准线方程为x=
(a>b>0)的一条准线方程为x=![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆C的方程;
(2)如图,设A为椭圆的上顶点,过点A作两条直线AM,AN,分别与椭圆C相交于M,N两点,且直线MN垂直于x轴.
① 设直线AM,AN的斜率分别是k1, k2,求k1k2的值;
② 过M作直线l1⊥AM,过N作直线l2⊥AN,l1与l2相交于点Q.试问:点Q是否在一条定直线上?若在,求出该直线的方程;若不在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com