Question

某校欲从两个素质拓展小组中选拔4个同学参加市教育局组织的2010年夏令营活动，已知甲组内有实力相当的1个女生和3个男生，乙组内有实力相当的2个女生和4个男生，现从甲、乙两个小组内各任选2个同学．
（1）求选出的4个同学中恰有1个女生的概率；
（2）设X为选出的4个同学中女生的个数，求X的分布列和数学期望．

Answer 1

分析：（1）选出的4个同学中恰有1个女生包括两种情况，从甲组内选出的2个同学均为男同学；从乙组内选出的2个同学中，1个是男同学，1个为女同学；从乙组内选出的2个同学均为男同学；从甲组内选出的2个同学中1个是男同学，1个为女同学，根据这两个事件是互斥事件，根据互斥事件的概率，得到结果．
（2）根据甲组内有实力相当的1个女生和3个男生，乙组内有实力相当的2个女生和4个男生，共有三个女生，所以选出的4个同学中女生的个数可能的取值是0、1、2、3，结合变量对应的事件做出概率，写出分布列和期望．

解答：解：（1）设“从甲组内选出的2个同学均为男同学；
从乙组内选出的2个同学中，1个是男同学，1个为女同学”为事件A，
“从乙组内选出的2个同学均为男同学；从甲组内选出的2个同学中1个是男同学，1个为女同学”为事件B，
由于事件A、B互斥，
且P（A）=

C 2 3 C 1 2 C 1 4

C 2 4 C 2 6

=

4

15

，P(B)=

C 1 3 C 2 4

C 2 4 C 2 6

=

1

5

，
∴选出的4个同学中恰有1个女生的概率为P(A+B)=P(A)+P(B)=

4

15

+

1

5

=

7

15

．

（2）X可能的取值为0，1，2，3，
P（X=0）=

1

5

，P（X=1）=

7

15

，P（X=2）=

3

10

，P（X=0）=

1

30

，
∴X的分布列为
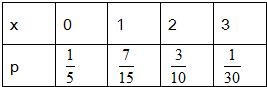
∴X的数学期望EX=1×

7

15

+2×

3

10

+3×

1

30

=

7

6

．

点评：本题考查离散型随机变量的分布列和期望，这种类型是近几年高考题中经常出现的，考查离散型随机变量的分布列和期望，大型考试中理科考试必出的一道问题．