
【题目】在一次数学考试中,第22题和第23题为选做题,规定每位考生必须且只须在其中选做一题,现有甲、乙、丙、丁4名考生参加考试,其中甲、乙选做第22题的概率均为![]() ,丙、丁选做第22题的概率均为
,丙、丁选做第22题的概率均为![]() .
.
(Ⅰ)求在甲选做第22题的条件下,恰有两名考生选做同一道题的概率;
(Ⅱ)设这4名考生中选做第22题的学生个数为X,求X的概率分布及数学期望.
【答案】(Ⅰ) ![]() (Ⅱ)
(Ⅱ) ![]()
【解析】试题分析:(Ⅰ)根据独立事件同时发生的概率公式及条件概率公式求解即可;(Ⅱ) X的所有可能取值为0、1、2、3、4,分别根据独立事件同时发生的概率公式及互斥事件的概率公式求得各随机变量发生的概率,列出分布列,根据期望公式求解即可.
试题解析:(Ⅰ)【方法一】记“甲选做第22题”为事件A;“恰有两名考生选做同一道题”为事件B.
由题意可计算, ![]() ,
, ![]() ,
,
所以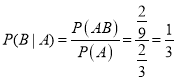 .
.
【方法二】在甲选做第22题的条件下,恰有两名考生选做同一道题,问题等价于“乙、丙、丁三人中有且只有一人选做第22题,其余两人选做第23题”,记为事件C.
由题意可计算, ![]() .
.
(Ⅱ) X的所有可能取值为0、1、2、3、4.
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
所以X的分布列为:
X | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
从而![]() .
.


科目:高中数学 来源: 题型:
【题目】已知过原点的动直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() .
.
(1)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)是否存在实数![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() 只有一个交点?若存在,求出
只有一个交点?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的方程为![]() +
+![]() =1,A、B为椭圆C的左、右顶点,P为椭圆C上不同于A、B的动点,直线x=4与直线PA、PB分别交于M、N两点;若D(7,0),则过D、M、N三点的圆必过x轴上不同于点D的定点,其坐标为________.
=1,A、B为椭圆C的左、右顶点,P为椭圆C上不同于A、B的动点,直线x=4与直线PA、PB分别交于M、N两点;若D(7,0),则过D、M、N三点的圆必过x轴上不同于点D的定点,其坐标为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=sin(ωx+φ)( ![]() )的最小正周期是π,若其图象向右平移
)的最小正周期是π,若其图象向右平移 ![]() 个单位后得到的函数为奇函数,则函数f(x)的图象( )
个单位后得到的函数为奇函数,则函数f(x)的图象( )
A.关于点 ![]() 对称
对称
B.关于点 ![]() 对称
对称
C.关于直线 ![]() 对称
对称
D.关于直线 ![]() 对称
对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ()的焦距为4,左、右焦点分别为
()的焦距为4,左、右焦点分别为![]() ,且
,且![]() 与抛物线
与抛物线![]() :
: ![]()
![]() 的交点所在的直线经过
的交点所在的直线经过![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]()
![]() 的直线
的直线![]()
![]() 与
与![]() 交于
交于![]() 两点,与抛物线
两点,与抛物线![]() 无公共点,求
无公共点,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2cos2x+ ![]() sin2x﹣1.
sin2x﹣1.
(1)求f(x)的最大值及此时的x值
(2)求f(x)的单调减区间
(3)若x∈[﹣ ![]() ,
, ![]() ]时,求f(x)的值域.
]时,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△AOB中,∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,△AOC为钝角三角形的概率是( )
A.0.2
B.0.4
C.0.6
D.0.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com