
【题目】已知函数![]() .
.
(1)若![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(2)若![]() ,且对于函数
,且对于函数![]() 的图象上两点
的图象上两点![]() ,
,![]()
![]() ,存在
,存在![]() ,使得函数
,使得函数![]() 的图象在
的图象在![]() 处的切线
处的切线![]() .求证;
.求证;![]() .
.
【答案】(1)见解析(2)见证明
【解析】
(1)对函数![]() 求导,分别讨论
求导,分别讨论![]() ,
,![]() 以及
以及![]() ,即可得出结果;
,即可得出结果;
(2)根据题意,由导数几何意义得到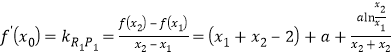 ,将证明
,将证明![]() 转化为证明
转化为证明![]() 即可,再令
即可,再令![]() ,设
,设![]()
![]() ,用导数方法判断出
,用导数方法判断出![]() 的单调性,进而可得出结论成立.
的单调性,进而可得出结论成立.
(1)解:易得,函数![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
令![]() ,得
,得![]() 或
或![]() .
.
①当![]() 时,
时,![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
![]() 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
此时,![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() .
.
②当![]() 时,
时,![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
![]() 或
或![]() 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
此时,![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() ,
,![]() .
.
③当![]() 时,
时,![]() 时,
时,![]() ,函数
,函数![]() 单调递增;
单调递增;
此时,![]() 的减区间为
的减区间为![]() .
.
综上,当![]() 时,
时,![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() :
:
当![]() 时,
时,![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() .
.![]() ;
;
当![]() 时,
时,![]() 增区间为
增区间为![]() .
.
(2)证明:由题意及导数的几何意义,得![]()
![]()
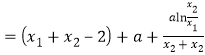
由(1)中![]() 得
得![]() .
.
易知,导函数![]()
![]() 在
在![]() 上为增函数,
上为增函数,
所以,要证![]() ,只要证
,只要证![]() ,
,
即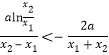 ,即证
,即证![]() .
.
因为![]() ,不妨令
,不妨令![]() ,则
,则![]()
![]() .
.
所以![]()
![]() ,
,
所以![]() 在
在![]() 上为增函数,
上为增函数,
所以![]() ,即
,即![]() ,
,
所以![]() ,即
,即![]() ,
,
即![]() .
.
故有![]() (得证).
(得证).


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,若椭圆经过点
,若椭圆经过点![]() ,且
,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设斜率为![]() 的直线
的直线![]() 与以原点为圆心,半径为
与以原点为圆心,半径为![]() 的圆交于
的圆交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,当
,当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用五种不同颜色(颜色可以不全用完)给三棱柱![]() 的六个顶点涂色,要求每个点涂一种颜色,且每条棱的两个端点涂不同颜色,则不同的涂色种数有( )
的六个顶点涂色,要求每个点涂一种颜色,且每条棱的两个端点涂不同颜色,则不同的涂色种数有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第18届国际篮联篮球世界杯将于2019年8月31日至9月15日在中国北京、广州等八座城市举行.届时,甲、乙、丙、丁四名篮球世界杯志愿者将随机分到![]() 、
、![]() 、
、![]() 三个不同的岗位服务,每个岗位至少有一名志愿者.
三个不同的岗位服务,每个岗位至少有一名志愿者.
(1)求甲、乙两人不在同一个岗位服务的概率;
(2)设随机变量![]() 为这四名志愿者中参加
为这四名志愿者中参加![]() 岗位服务的人数,求
岗位服务的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家规定,疫苗在上市前必须经过严格的检测,并通过临床实验获得相关数据,以保证疫苗使用的安全和有效.某生物制品硏究所将某一型号疫苗用在动物小白鼠身上进行科研和临床实验,得到统计数据如下:
未感染病毒 | 感染病毒 | 总计 | |
未注射疫苗 | 40 | p | x |
注射疫苗 | 60 | q | y |
总计 | 100 | 100 | 200 |
现从未注射疫苗的小白鼠中任取1只,取到“感染病毒”的小白鼠的概率为![]() .
.
(1)求![]() 列联表中的数据p,q,
列联表中的数据p,q,![]() ,
,![]() 的值;
的值;
(2)能否有![]() 把握认为注射此种疫苗有效?
把握认为注射此种疫苗有效?
(3)在感染病毒的小白鼠中,按未注射疫苗和注射疫苗的比例抽取5只进行病例分析,然后从这五只小白鼠中随机抽取3只对注射疫苗情况进行核实,求至少抽到2只为未注射疫苗的小白鼠的概率. 附:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,下图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
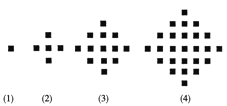
(1) 求出![]() ,
,![]() ,
,![]() 并猜测
并猜测![]() 的表达式;
的表达式;
(2) 求证:![]() +
+![]() +
+![]() +…+
+…+![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年被称为“新高考元年”,随着上海、浙江两地顺利实施“语数外+3”新高考方案,新一轮的高考改革还将继续在全国推进。辽宁地区也将于2020年开启新高考模式,今年秋季入学 的高一新生将面临从物理、化学、生物、政治、历史、地理等6科中任选三科(共20种选法)作为 自己将来高考“语数外+3 ”新高考方案中的“3”。某地区为了顺利迎接新高考改革,在某学校理科班的200名学生中进行了“学生模拟选科数据”调查,每个学生只能从表格中的20种课程 组合选择一种学习。模拟选课数据统计如下表:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
组合学科 | 物化生 | 物化政 | 物化历 | 物化地 | 物生政 | 物生历 | 物生地 |
人数 | 20人 | 5人 | 10人 | 10人 | 10人 | 15人 | 10人 |
序号 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
组合学科 | 物政历 | 物政地 | 物历地 | 化生政 | 化生历 | 化生地 | 化政历 |
人数 | 5人 | 0人 | 5人 | ... | 40人 | ... | ... |
序号 | 15 | 16 | 17 | 18 | 19 | 20 | |
组合学科 | 化政地 | 化历地 | 生政历 | 生政地 | 生历地 | 政历地 | 总计 |
人数 | ... | ... | ... | ... | ... | ... | 200人 |
为了解学生成绩与学生模拟选课情之间的关系,用分层抽样的方法从这200名学生中抽取40人的样本进行分析.
(1)样本中选择组合12号“化生历”的有多少人?样本中选择学习物理的有多少人?
(2)从样本选择学习地理且学习物理的学生中随机抽取3人,求这3人中至少有1人还要学习生物的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.
(Ⅰ)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(Ⅱ)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作.
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设M为事件“抽取的2名同学来自同一年级”,求事件M发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com