
【题目】设函数![]() 在
在![]() 上有定义,实数
上有定义,实数![]() 和
和![]() 满足
满足![]() .若
.若![]() 在区间
在区间![]() 上不存在最小值,则称
上不存在最小值,则称![]() 在区间
在区间![]() 上具有性质P.
上具有性质P.
(1)当![]() ,且
,且![]() 在区间
在区间![]() 上具有性质P,求常数C的取值范围;
上具有性质P,求常数C的取值范围;
(2)已知![]() ,且当
,且当![]() 时,
时,![]() ,判别
,判别![]() 在区间
在区间![]() 上是否具有性质P;
上是否具有性质P;
(3)若对于满足![]() 的任意实数
的任意实数![]() 和
和![]() ,
,![]() 在区间
在区间![]() 上具有性质P,且对于任意
上具有性质P,且对于任意![]() ,当
,当![]() 时,有:
时,有:![]() ,证明:当
,证明:当![]() 时,
时,![]() .
.
【答案】(1)![]() ;(2)具有性质
;(2)具有性质![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)由对称轴![]() 可得;
可得;
(2)求出![]() 在
在![]() 上的函数解析式,判断出函数在
上的函数解析式,判断出函数在![]() 上后一个区间上的函数值都比前一个区间上的函数值大,从而函数最小值(如果有)只能在第一个区间
上后一个区间上的函数值都比前一个区间上的函数值大,从而函数最小值(如果有)只能在第一个区间![]() 上取得,但在
上取得,但在![]() 上函数无最小值,因此可得出结论;
上函数无最小值,因此可得出结论;
(3)由绝对值的性质知![]() ,即
,即![]() 夹在
夹在![]() 和
和![]() 之间,如果
之间,如果![]() ,则
,则![]() 在
在![]() 上有最小值,不具有性质
上有最小值,不具有性质![]() ,与已知矛盾,从而只能是
,与已知矛盾,从而只能是![]() ,然后只要说明对任意的
,然后只要说明对任意的![]() ,一定有
,一定有![]() ,
,![]() ,则必有
,则必有![]() ,而
,而![]() ,因此结论显然成立.
,因此结论显然成立.
(1)![]() ,对称轴
,对称轴![]() ,当
,当![]() 时,
时,![]() 是最小值,当
是最小值,当![]() 时,
时,![]() 是最小值,只有当
是最小值,只有当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 是递增,无最小值;
是递增,无最小值;
(2)![]() 时,
时,![]() ,
,![]() ,同理
,同理![]() 时,
时,![]() ,
,![]() ,
,
即 ,易知当
,易知当![]() 时,
时,![]() 是最大值,而对任意的
是最大值,而对任意的![]() ,
,![]() ,
,![]() ,都有
,都有![]() 恒成立,
恒成立,
∴![]() 时,若
时,若![]() 有最小值,则只有在
有最小值,则只有在![]() 时取得,但当
时取得,但当![]() 时,
时,![]() 是减函数,无最小值,∴
是减函数,无最小值,∴![]() 在
在![]() 上无最小值,具有性质
上无最小值,具有性质![]() ;
;
(3)对于任意![]() ,当
,当![]() 时,
时,
有:![]() ,
,
∴![]() ,
,
若![]() 成立,则
成立,则![]() 在
在![]() 上有最小值
上有最小值![]() ,不具有性质
,不具有性质![]() ,不合题意,所以只有
,不合题意,所以只有![]() .
.
显然有![]() ,
,
则对任意的![]() ,则一定存在
,则一定存在![]() ,使得
,使得![]() 则
则![]() ,
,![]() ,
,
∴![]() ,即
,即![]() .
.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】《中国诗词大会》是由CCTV-10自主研发的一档大型文化益智节目,以“赏中华诗词,寻文化基因品生活之美”为宗旨,带动全民重温经典、从古人的智慧和情怀中汲取营养、涵养心灵,节目广受好评还因为其颇具新意的比赛规则:每场比赛,106位挑战者全部参赛,分为单人追逐赛和擂主争霸赛两部分单人追逐赛的最终优胜者作为攻擂者与守擂擂主进行比拼,竞争该场比赛的擂主,擂主争霸赛以抢答的形式展开,共九道题,抢到并回答正确者得一分,答错则对方得一分,先得五分者获胜,成为本场擂主,比赛结束已知某场擂主争霸赛中,攻擂者与守擂擂主都参与每一次抢题且两人抢到每道题的概率都是![]() ,攻擂者与守擂擂主正确回答每道题的概率分别为
,攻擂者与守擂擂主正确回答每道题的概率分别为![]() ,
,![]() ,且两人各道题是否回答正确均相互独立.
,且两人各道题是否回答正确均相互独立.
(1)比赛开始,求攻擂者率先得一分的概率;
(2)比赛进行中,攻擂者暂时以![]() 领先,设两人共继续抢答了
领先,设两人共继续抢答了![]() 道题比赛结束,求随机变量
道题比赛结束,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥S-ABCD中,四边形ABCD是菱形,![]() ,
,![]() ,点P,Q,M分别是线段SD,PD,AP的中点,点N是线段SB上靠近B的四等分点.
,点P,Q,M分别是线段SD,PD,AP的中点,点N是线段SB上靠近B的四等分点.
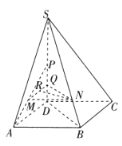
(1)若R在直线MQ上,求证:![]() 平面ABCD;
平面ABCD;
(2)若![]() 平面ABCD,求平面SAD与平面SBC所成的锐二面角的余弦值.
平面ABCD,求平面SAD与平面SBC所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F为抛物线y2=x的焦点,点A,B在该抛物线上且位于x轴的两侧,![]() (其中O为坐标原点),则△ABO与△AFO面积之和的最小值是________.
(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是________.
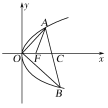
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 和
和![]() 均是等腰直角三角形,
均是等腰直角三角形,![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
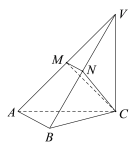
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 为等边三角形,
为等边三角形,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,平面
,平面![]() 平面ABD,点E与点D在平面ABC的同侧,且
平面ABD,点E与点D在平面ABC的同侧,且![]() ,
,![]() .点F为AD中点,连接EF.
.点F为AD中点,连接EF.

(1)求证:![]() 平面ABC;
平面ABC;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<![]() )的部分图象如图所示.
)的部分图象如图所示.
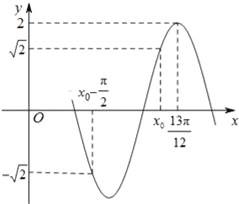
(Ⅰ)写出函数f(x)的解析式及x0的值;
(Ⅱ)求函数f(x)在区间[﹣![]() ,
,![]() ]上的最大值与最小值.
]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国工业经济发展迅速,工业增加值连年攀升,某研究机构统计了近十年(从2008年到2017年)的工业增加值(万亿元),如下表:
年份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
工业增加值 | 13.2 | 13.8 | 16.5 | 19.5 | 20.9 | 22.2 | 23.4 | 23.7 | 24.8 | 28 |
依据表格数据,得到下面的散点图及一些统计量的值.
|
|
|
|
|
5.5 | 20.6 | 82.5 | 211.52 | 129.6 |
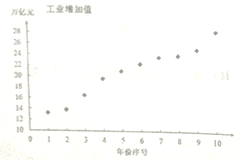
(1)根据散点图和表中数据,此研究机构对工业增加值![]() (万亿元)与年份序号
(万亿元)与年份序号![]() 的回归方程类型进行了拟合实验,研究人员甲采用函数
的回归方程类型进行了拟合实验,研究人员甲采用函数![]() ,其拟合指数
,其拟合指数![]() ;研究人员乙采用函数
;研究人员乙采用函数![]() ,其拟合指数
,其拟合指数![]() ;研究人员丙采用线性函数
;研究人员丙采用线性函数![]() ,请计算其拟合指数,并用数据说明哪位研究人员的函数类型拟合效果最好.(注:相关系数
,请计算其拟合指数,并用数据说明哪位研究人员的函数类型拟合效果最好.(注:相关系数![]() 与拟合指数
与拟合指数![]() 满足关系
满足关系![]() ).
).
(2)根据(1)的判断结果及统计值,建立![]() 关于
关于![]() 的回归方程(系数精确到0.01);
的回归方程(系数精确到0.01);
(3)预测到哪一年的工业增加值能突破30万亿元大关.
附:样本
![]() 的相关系数
的相关系数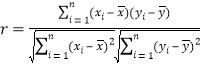 ,
,
![]() ,
,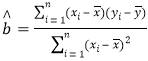 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com