
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 5π |
| 12 |
| π |
| 4 |
| π |
| 2 |
| π |
| 3 |
| 2π |
| ω |
| 5π |
| 12 |
| 5π |
| 12 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 5π |
| 12 |
| π |
| 12 |
| 5π |
| 12 |
| π |
| 4 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:

| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
. |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 4 |
| y2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某班50名学生在一次百米跑测试中,成绩全部介于13秒与18秒之间,将测度结果按如下方式分成五组:第一组[13,14),第二组[14,15),…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
某班50名学生在一次百米跑测试中,成绩全部介于13秒与18秒之间,将测度结果按如下方式分成五组:第一组[13,14),第二组[14,15),…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:
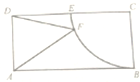 如图,矩形ABCD中,AB=2,BC=1,以点C为圆心,CB为半径的圆与边DC交于点E,F是
如图,矩形ABCD中,AB=2,BC=1,以点C为圆心,CB为半径的圆与边DC交于点E,F是 |
| BE |
查看答案和解析>>
科目:高中数学 来源: 题型:
| k |
| 20x+100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com