Question

【题目】如图，三棱柱ABC﹣A1B1C1中，侧面BB1C1C为菱形，AB⊥B1C．
（Ⅰ）证明：AC=AB1；
（Ⅱ）若AC⊥AB1 ， ∠CBB1=60°，AB=BC，求二面角A﹣A1B1﹣C1的余弦值．

Answer 1

【答案】解：（Ⅰ）连结BC1，交B1C于点O，连结AO，

∵侧面BB1C1C为菱形，

∴BC1⊥B1C，且O为BC1和B1C的中点，

又∵AB⊥B1C，∴B1C⊥平面ABO，

∵AO平面ABO，∴B1C⊥AO，

又B10=CO，∴AC=AB1，

（Ⅱ）∵AC⊥AB1，且O为B1C的中点，∴AO=CO，

又∵AB=BC，∴△BOA≌△BOC，∴OA⊥OB，

∴OA，OB，OB1两两垂直，

以O为坐标原点， 的方向为x轴的正方向，| |为单位长度，

的方向为y轴的正方向， 的方向为z轴的正方向建立空间直角坐标系，

∵∠CBB1=60°，∴△CBB1为正三角形，又AB=BC，

∴A（0，0， ），B（1，0，0，），B1（0， ，0），C（0， ，0）

∴ =（0， ， ）， = =（1，0， ）， = =（﹣1， ，0），

设向量 =（x，y，z）是平面AA1B1的法向量，

则 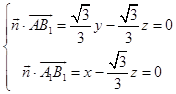，可取 =（1， ， ），

同理可得平面A1B1C1的一个法向量 =（1，﹣ ， ），

∴cos＜ ， ＞= = ，

∴二面角A﹣A1B1﹣C1的余弦值为

【解析】（Ⅰ）连结BC1，交B1C于点O，连结AO，可证B1C⊥平面ABO，可得B1C⊥AO，B10=CO，进而可得AC=AB1；（Ⅱ）以O为坐标原点， 的方向为x轴的正方向，| |为单位长度， 的方向为y轴的正方向， 的方向为z轴的正方向建立空间直角坐标系，分别可得两平面的法向量，可得所求余弦值．