
分析 易得总的基本事件有36种,由向量垂直可得m-n=0,共6种,由概率公式可得.
解答 解:将一颗质地均匀的骰子先后抛掷2次出现的点数情况共6×6=36种,
由$\overrightarrow a=({m-2,2-n})$,向量$\overrightarrow b=({1,1})$,
由于向量$\overrightarrow a⊥\overrightarrow b$,
所以m-2+2-n=0,即m-n=0,
上述满足m-n=0的有(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)共6种,
故所求概率为P=$\frac{6}{36}$=$\frac{1}{6}$
故答案为:$\frac{1}{6}$
点评 本题考查古典概型及其概率公式和向量垂直的条件,属基础题.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{9}{16}$x | B. | y=±$\frac{3}{4}$x | C. | y=±$\frac{16}{9}$x | D. | y=±$\frac{4}{3}$x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
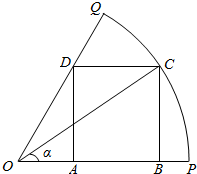 如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形,记∠COP=α,
如图,已知OPQ是半径为1,圆心角为$\frac{π}{3}$的扇形,C是扇形弧上的动点,ABCD是扇形的内接矩形,记∠COP=α,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 0 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com